|
|
FlexPDEを使って偏微分方程式の固有値や固有関数を求めることもできます。
上で示した時間依存型の同次熱流体方程式について考えてみましょう。
境界条件についても同次型のもの、すなわち
を想定します。
今、次のような変数分離型の解を求めたいとします。
このとき偏微分方程式は次のようになります。
この方程式が自明以外の解を持つときの
FlexPDEに固有値問題を解かせるには定常状態用のベーシックなスクリプトに対し次のような変更を加える必要があります。
TITLE 'Modal Heat Flow Analysis' SELECT modes=4 VARIABLES Phi { the temperature } DEFINITIONS K = 1 { default conductivity } R = 0.5 { blob radius } EQUATIONS Div(k*grad(Phi)) + LAMBDA*Phi = 0 BOUNDARIES REGION 1 'box' START(-1,-1) VALUE(Phi)=0 LINE TO (1,-1) NATURAL(Phi)=0 LINE TO (1,1) VALUE(Phi)=0 LINE TO (-1,1) NATURAL(Phi)=0 LINE TO CLOSE REGION 2 'blob' { the embedded blob } k = 0.2 { This value makes more interesting pictures } START 'ring' (R,0) ARC(CENTER=0,0) ANGLE=360 TO CLOSE PLOTS CONTOUR(Phi) VECTOR(-k*grad(Phi)) ELEVATION(Phi) FROM (0,-1) to (0,1) ELEVATION(Normal(-k*grad(Phi))) ON 'ring' END
FlexPDEによって出力される解は次のような特徴を持ったものとなります。
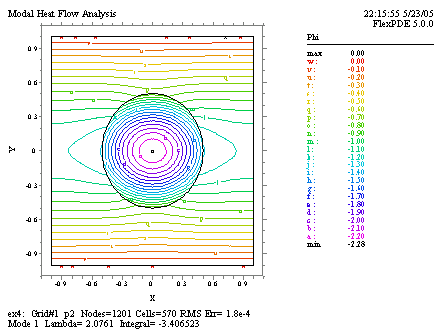
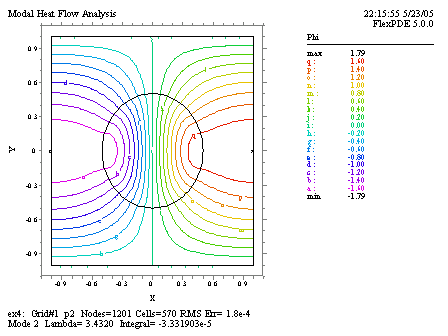
最初の2つの固有値に対応した等温線図は次のようになります。
|
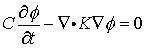
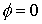
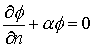
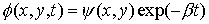
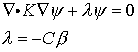
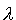 と
と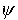 をそれぞれ系の固有値、固有関数と呼びます。偏微分方程式に対する一般解は、非同次境界条件を満たす一つの特解とこれら固有関数を組み合わせたものとして表現できます。
をそれぞれ系の固有値、固有関数と呼びます。偏微分方程式に対する一般解は、非同次境界条件を満たす一つの特解とこれら固有関数を組み合わせたものとして表現できます。