構造方程式モデリングの概要

事例1：品質管理

注意事項：以降の全ての事例は、SEM（構造方程式モデリング）が各分野でどのように応用できるかをイメージしやすくするために、極めて単純化した設定のもとで架空の解析例を示したものです。記載した示唆・解釈は例示を目的として人工的に作成されたものであり、通説や実際の状況を反映しているものではない旨、ご了承ください。

様々な要因のうち何が製品品質に影響を与えるか、構造方程式モデリング（SEM）で把握してみませんか？

課題提議：ある会社が、製品品質向上のため会社全体での意識改善を行おうとしています。しかし、どの活動が製品の品質改善に貢献しているのか？経営層の支援や現場の連携が成果にどう影響するのか？を数字で説明できず、改善行動の優先順位付けが“経験と勘”に頼りがちという課題がありました。

SEMの利用：研究チームは各工場の管理職・作業者にアンケートを実施しました。アンケート結果を通じ、各工場で下記表1に示した観測変数①～④を測定・点数化し、考慮した潜在変数を1つ交えてSEMを実行しました。
SEM実行例の結果を図2に示しています。特に、検査合格率と返品率に関係する潜在変数を「品質管理能力」と解釈しました。

①	経営層からの支援の度合い
②	他工程との連携の度合い
③	品質指標1：検査合格率
④	品質指標2：返品率
潜在変数(③+④)	「品質管理能力」と解釈

表1：観測変数①～④と、考慮した潜在変数

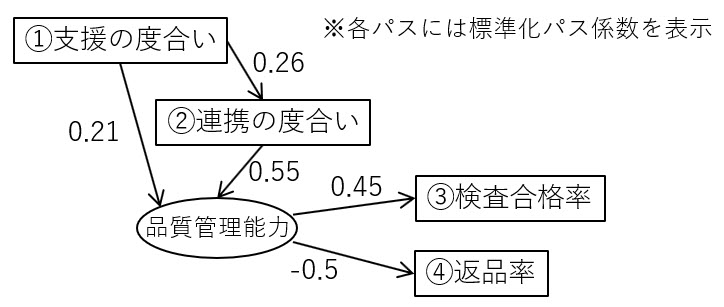
図2：設計したパス図と、最適化により得られたパス係数

結果の解釈：各項目間のパスの係数を読み解くと、例えば以下のような示唆が得られます。
A）経営層からの支援により，工程間の連携が改善しうる。
B）潜在的な「品質管理能力」は検査合格率に良い影響を与えうる。この能力が高ければ返品率を下げうる。
C）経営層の支援の度合いよりも、他工程との連携が潜在的な「品質管理能力」に大きな影響を与えうる。

事例2：経済・金融における応用

課題提議：ある企業では、社員の金融リテラシー向上を目的とした支援プログラム導入を検討しています。福利厚生の一環として、支援プログラムが社員の計画的な資産形成につながることを期待しています。しかし実際にはどの項目がリテラシー向上および実際の資産形成に効果的なのかなどが明確に把握できていません。

SEMの利用：支援チームでは各社員ごとに基礎的・応用的な金融知識のテスト、学歴、および金融情報の収集頻度を調べ、また貯蓄額と社員の投資収益率を調べました。この際、テスト得点・学歴・情報収集頻度の背後にある因子を金融リテラシー、貯蓄額・投資収益率の背後にある因子を資産形成能力と解釈し、以下のパス図を書いてSEMを実行すると以下の係数が得られました。

図：設計したパス図と、最適化により得られたパス係数

各項目間のパスの係数を読み解くと、例えば以下のような示唆が得られます。
A）金融リテラシーは資産形成能力に強い影響を与えうる。
B）基礎的な内容よりも，より応用的な知識のほうが金融リテラシーへの影響力が大きいと考えられる。
C）学歴の金融リテラシーへの影響力は限定的であると考えられる。

事例3：マーケティングにおける応用

課題提議：ある企業のマーケティング部門では、SNSによる情報発信やweb広告の出稿に力を入れようとしています。しかし実際には、SNSとweb広告のどちらが売り上げに大きく貢献しているのかなどが明確に把握できていません。

SEMの利用：研究チームは、様々な商品についてSNS投稿数、SNSエンゲージメント率（=いいねや共有などをされた割合）、web広告のクリック率、商品ページ訪問者数、および一か月間での当該商品の購入件数を調べました。SNS関係の背後にある因子をSNS効果、web広告関係の背後にある因子をweb広告効果と解釈し、以下のパス図を書いてSEMを実行すると以下の係数が得られました。

図：設計したパス図と、最適化により得られたパス係数

各項目間のパスの係数を読み解くと、例えば以下のような示唆が得られます。
A）SNS効果とweb広告効果には一定の正の相関がある。
B）SNS効果はweb広告効果よりも影響力が大きいと考えられる。
C）特にSNS投稿数はSNS効果に強い影響を及ぼしうることが示唆され、SNS投稿数を伸ばすと購入件数も伸びうることが期待される。

はじめに

　構造方程式モデリング（SEM, Structural Equation Modeling）とは、仮説に基づいて変数間の関係をモデル化し、そのモデルをデータに当てはめて検証する分析手法です。共分散構造分析とも呼ばれます。心理学や計量経済学などの分野で利用され、アンケート結果のデータなどから、定量的に計測できない変数間の関係性をモデル化することができます。

　構造方程式モデリングでは、観測可能な変数（観測変数）と観測されない潜在的な変数（潜在変数）の因果関係を仮説に基づいてモデル化します。潜在変数間の関係を表現することができ、仮説の妥当性を検証する際に有用な分析手法です。

　以下では、構造方程式モデリングの概要についてご紹介します。

SEMで表現できる統計モデル
パス図によるモデルの表現
多重指標モデル
分析の流れ
まとめ

1.　SEMで表現できる統計モデル

　さまざまな種類の統計モデルを表現するための非常に柔軟な手法です。 SEMを使用することで、観測データや潜在変数間の複雑な関係をモデル化し、因果関係や相関を解析することができます。
　以下は、SEMを用いて表現できる代表的な統計モデルの一例です。

パス解析: 複数の変数間の因果関係を図式化し、統計的に検証する手法です。回帰分析を拡張し、直接的・間接的な影響を明確にし、因果モデルの妥当性を確認します。
媒介分析: ある変数が他の変数間の関係にどのように影響を与えるかを調べる手法です。独立変数が従属変数に与える影響が、媒介変数を通じてどのように伝わるかを解析します。

確認的因子分析: 事前に設定した因子構造に基づいてデータを検証する手法です。観測変数が特定の因子にどのように関連するかを確認し、理論的なモデルの適合度を評価します。
多重指標モデル: 潜在変数を複数の観測変数（指標）で測定し、その関係性を分析する方法です。指標間の相関を考慮し、潜在変数の特性をより精度高く評価します。

2.　パス図によるモデルの表現

　変数間の関係を表すには、パス図を用います。観測変数、潜在変数、誤差変数を四角形、楕円、円などの図形で表現し、各変数間（図形）を矢印でつなぐことで因果関係や相関関係を表現します。

　構造方程式モデリングが実装された統計解析ソフトウェアでは、パス図を描くことでモデルを表現できるものが多く、変数間の複雑な関係を簡潔に表現できます。

　右図は、統計解析ソフトウェアStataで記述した構造方程式モデリングの一例です。

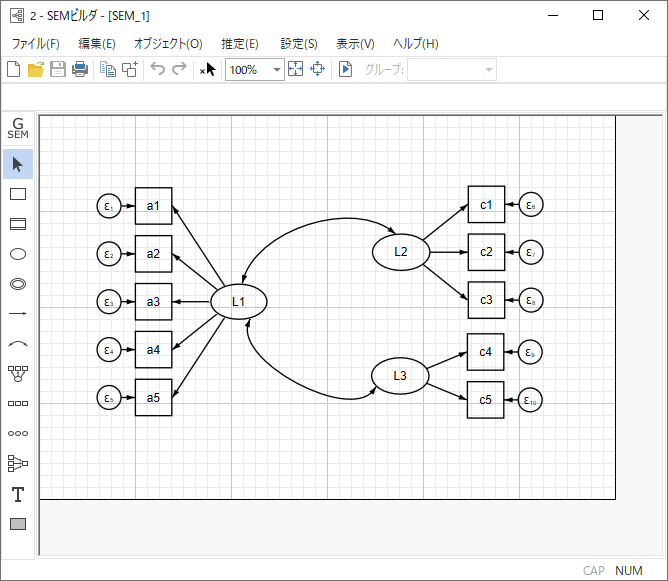
3.　多重指標モデル

　多重指標モデルは、複数の観測変数（指標）を使用して、複数の潜在変数（因子）を測定するモデルです。測定モデルと構造モデルの2つの主要な部分から構成されます。

測定モデル（Measurement Model）: 潜在変数は直接観測できない概念（例：知能、満足度、社会的支援など）で、観測変数はその潜在変数を示す実際のデータ（例：テスト結果、アンケートの項目、観察値など）です。測定モデルでは、観測変数がどの潜在変数に関連しているか、そしてどれくらいの重み（因子負荷）を持つかを特定します。
構造モデル（Structural Model）: 潜在変数間の因果関係を表現します。変数がどのように相互に影響を与え合うかを示し、因果関係のパス（矢印）を定義することによって、変数間の関係を表現にします。

構造方程式モデリングにおける多重指標モデルは、複数の観測変数を使って潜在変数を測定し、これらの潜在変数間の関係を分析する方法です。これにより、観測できない心理的な要因を考慮に入れつつ、因果関係をモデル化できるため、複雑なデータの解析に非常に強力なツールとなります。

4.　分析の流れ

構造方程式モデリングの分析手順は次のとおりです。

仮説に基づいて変数間の関係をモデル化する
構築したモデルをデータに当てはめる
モデルがデータに適合しているか適合度を確認する
推定結果から考察を行う
モデルの改善と再評価

　モデルの適合度を評価するために、CFI（比較適合指数）、TLI（トール・ルイス指数）、RMSEA（平均二乗誤差）などの適合度指標を確認します。
　初期のモデルが適合しない場合にモデルを修正することがありますが、理論的根拠を伴った変更を行うべきです。

5.　まとめ

　構造方程式モデリング（SEM）は、観測されたデータと潜在変数（直接観測できない概念）間の複雑な関係を明示化するための強力な分析手法です。 SEMでは、測定モデルと構造モデルを組み合わせることで、潜在変数間の因果関係を推定し、データの背後にある構造を解明できます。
　これにより、心理学、社会学、マーケティングなどの分野で、消費者の態度や行動、企業の戦略的意思決定、健康状態の評価などを定量的に分析できます。また、複数の指標を使用して、データ間の複雑な相互作用や因果関係を明示的に示すことができる点が大きな利点です。