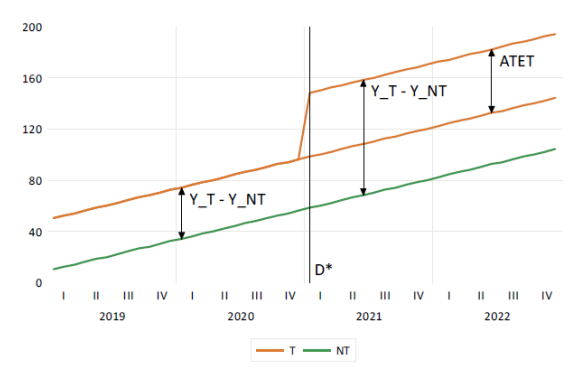
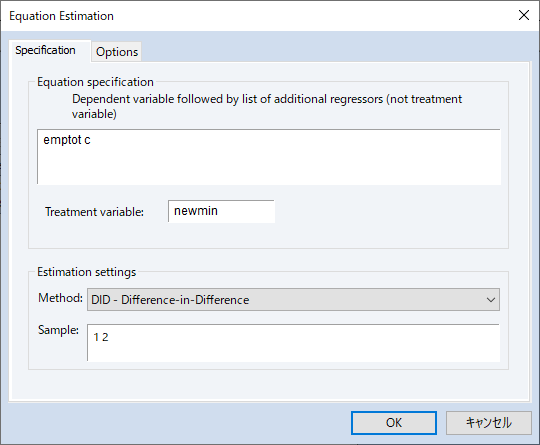
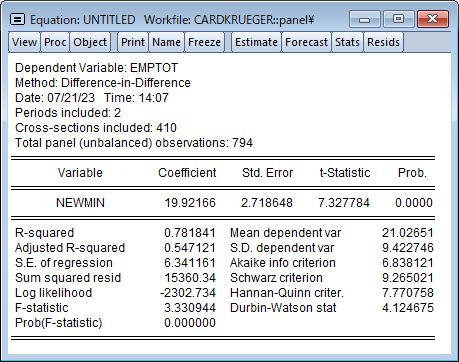
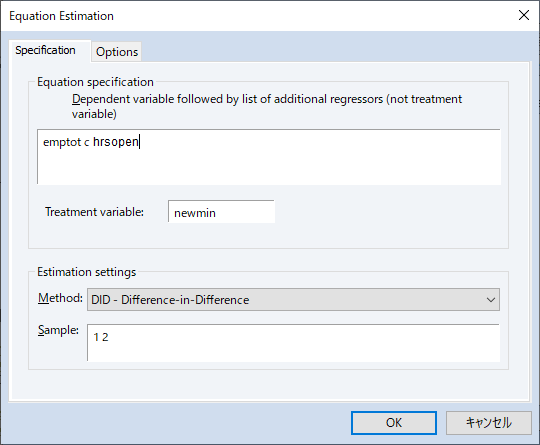
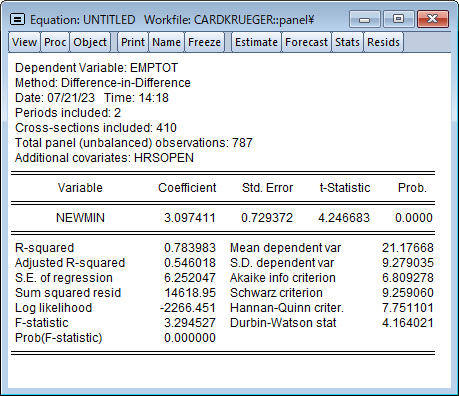
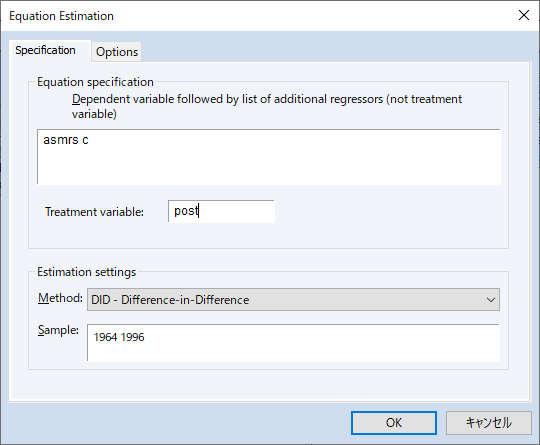
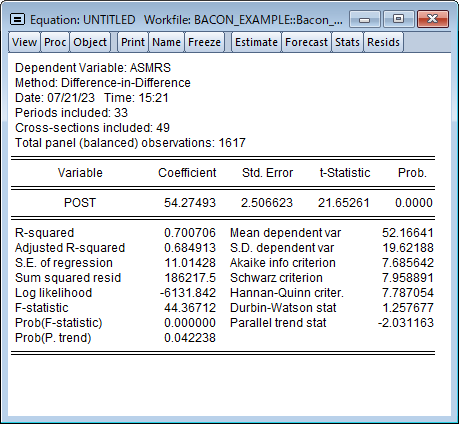
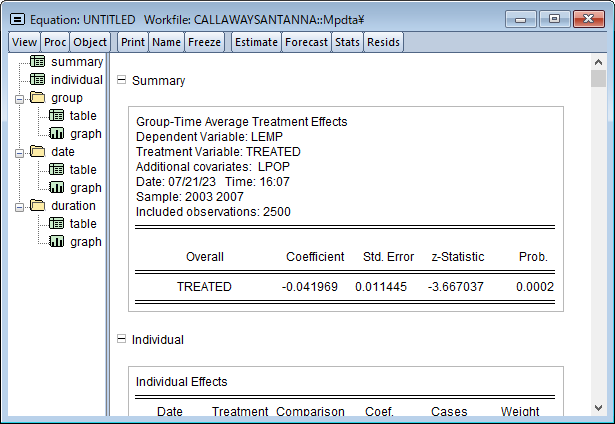
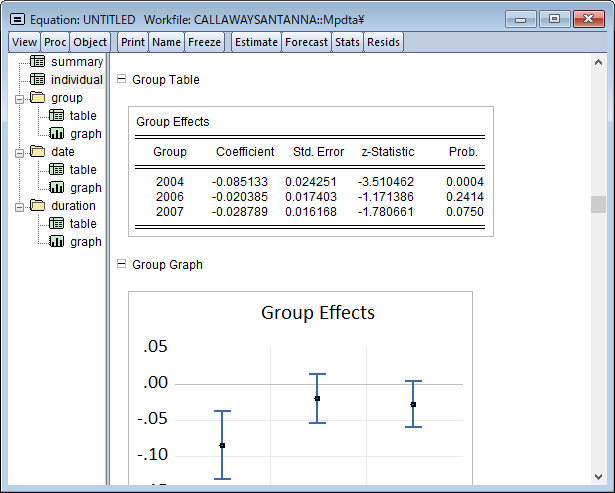
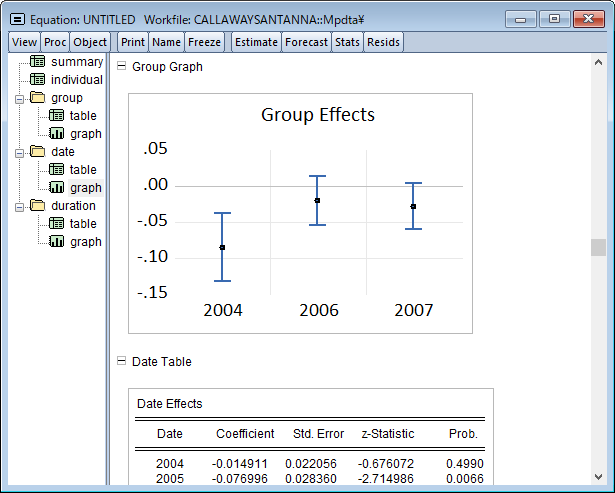
EViews 13では、差分の差分(DiD)推定をサポートしました。これは個体に行われた処置の平均的なインパクトを推定する, 因果推論におけるポピュラーな方法です。
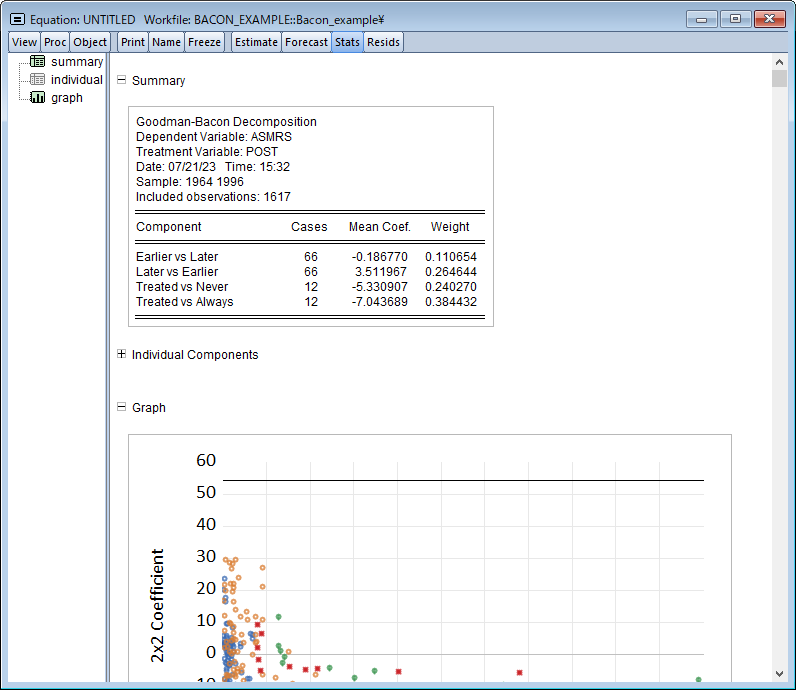
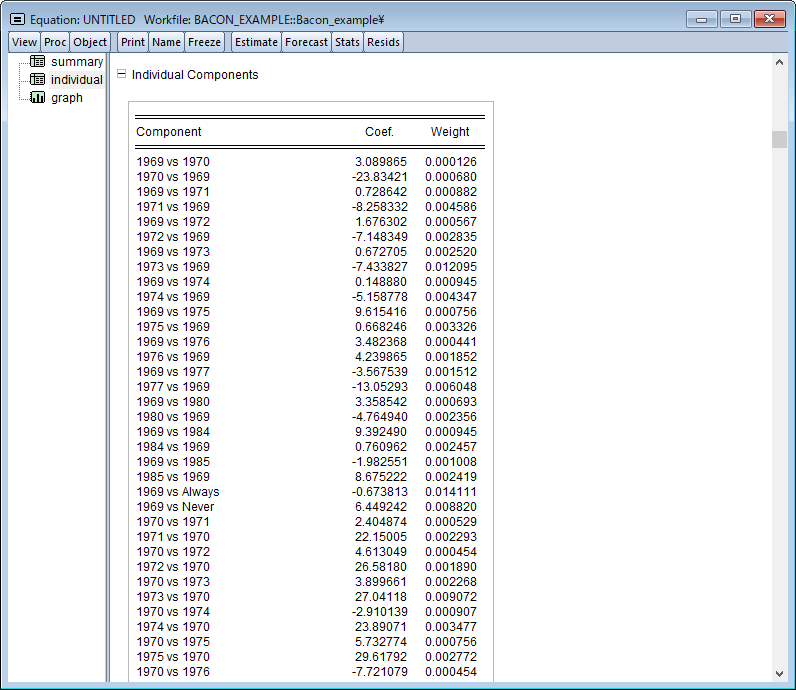
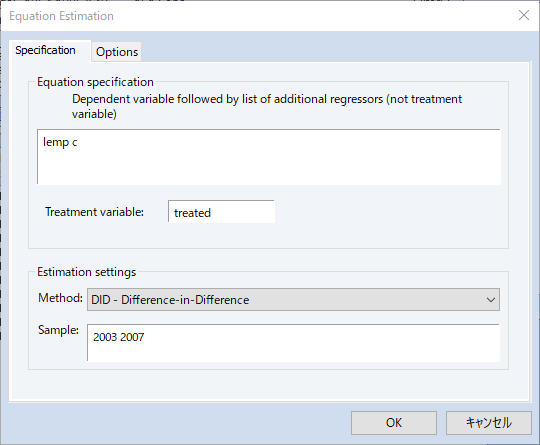
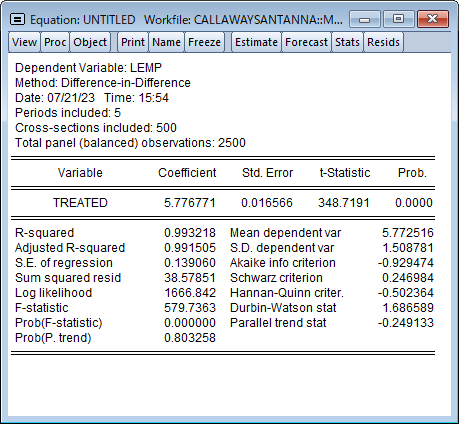
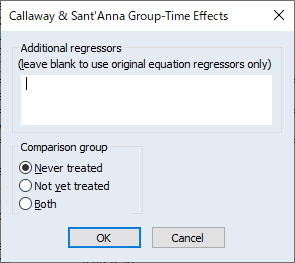
DiDは通常、処置効果が個体間・時間を通じて一定であることを仮定しますが、個体毎に処置効果が異なることが疑われる場合、EViewsは処置効果の分解やトレンド検定をサポートします。このページでは、差分の差分モデルの推定について、Goodman-Bacon (2021), Callaway and Sant’Anna (2021)および Brusyak,Jarael,and Spiess (2021)による, 一般的な 2 方向の固定効果(TWFE)を持つ手法を利用したDiDモデルの推定を紹介します。このページは、EViews 13 ユーザーズガイドIIを参考にしています。