適用分野
熱流体 | 応力解析 | 流体力学 | 化学反応 | 電磁気学 | 拡散
熱流体
木枠の窓に関するクロスセクションのモデル解析例をここで紹介します。 モデル全体は伝導率の異なる17の領域で構成されています。 窓の外側と内側では70度の温度差があるものとします。
自動メッシュ (クリックして拡大)
温度分布
応力解析
穴の開いたテンションバーの変形モデルを例として示します。 バーにおけるXとYの変位を求める同時偏微分方程式の例を紹介します。
dx(Sx) + dy(Txy) + Fx = 0
dx(Txy) + dy(Sy) + Fy = 0
Sx と Sy はXおよびY方向の応力です. Txy は剪断応力で, Fx と Fy はXおよびY方向の体積力です.
Sx = C11*dx(U) + C12*dy(V) + C13*[dy(U) + dx(V)]
Sy = C12*dx(U) + C22*dy(V) + C23*[dy(U) + dx(V)]
Txy = C13*dx(U) + C23*dy(V) + C33*[dy(U) + dx(V)]
ここでCnnは材料の補助方程式です。
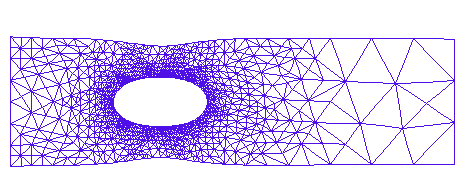
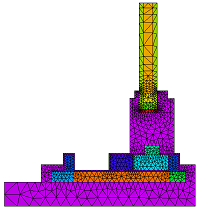
適合型調整グリッドの最終出力
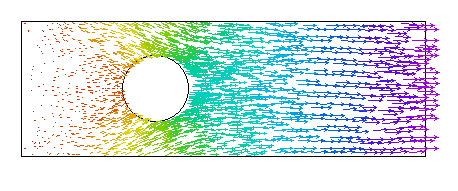
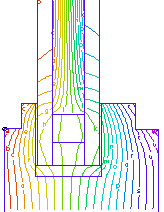
ベクトル変位フィールド
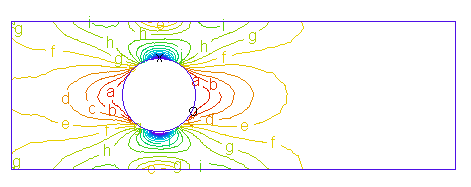
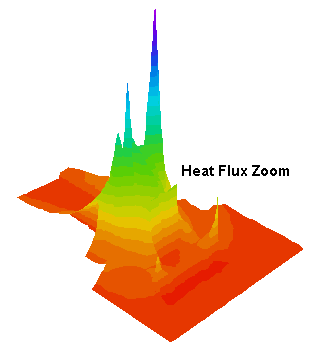
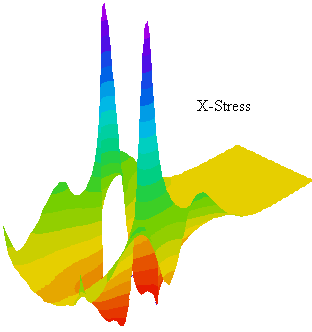
X方向の応力
流体力学
2次元チャネルの粘性流体モデルの例を紹介します。。FlexPDEはチャネルの終端に一定圧力のある流体のXY速度を求めることができます。 このモデルにおけるレイノルズ数は約20とします。
2次元直交座標における定常非圧縮流体のナビエ-ストークス方程式を次に示します。
rho*[dt(U) + U*dx(U) + V*dy(U)] = mu*div(grad(U)) - dx(P)
rho*[dt(V) + U*dx(V) + V*dy(V)] = mu*div(grad(V)) - dy(P)
連続方程式は次の通りです。
dx(U) + dy(V) = 0.
UとVはそれぞれXとYの速度であり, Pは圧力(連続方程式の代理変数), rhoは密度, muは粘度です.
適合調整メッシュ:
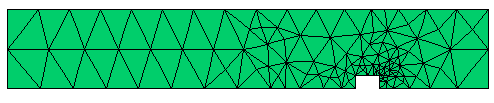
流体速度:
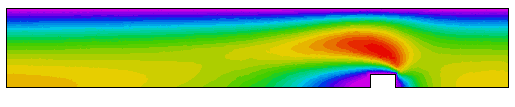
圧力:
化学反応
開放管化学反応器の中を流れる気体の動きを示すモデルを紹介します。化学反応速度は温度の指数に比例し、発火点に達すると気体は爆発します。 管の両側には発火を誘発する, 熱の高い部分が存在します。 ここでは敢えて四分円部分をモデル化します。 温度と化学濃度を示す2つの同時方程式を利用します。
dt(T) = div(grad(T)) + a*(1-C)*exp(G-G/T)
dt(C) = div(grad(C)) + b*(1-C)*exp(G-G/T)
T は温度, C は濃度, a, b, G は定数です.
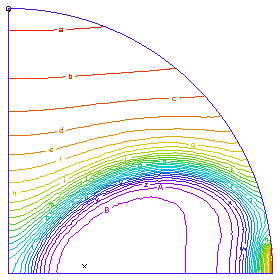
前方の熱の高い領域が管の中で広がる様子が分かります。 (Time = 0.25 sec)
管の複数ポイントにおける温度変化
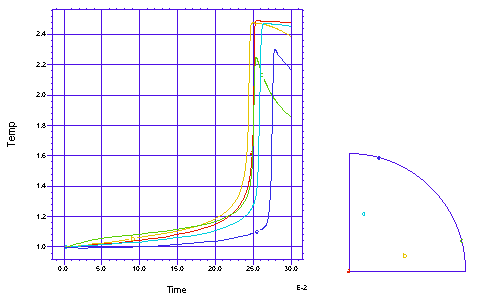
電磁気学
永久磁石を中心に据えた磁場モデルの例を紹介します。
PDEは次のような式とします。
curl(curl(A)-P)/mu) + J = 0,
Aは磁気ベクトルポテンシャル, Pは磁化率, Jは電流密度, muは透磁率とします。
適合型グリッド(クリックして拡大)
磁気ポテンシャルA
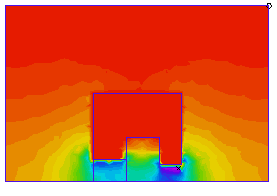
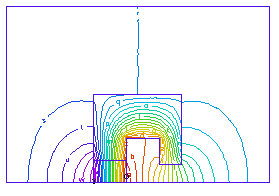
磁場の強さ
拡散
添加物が固体中を熱によって拡散するときの様子をモデル化した例を紹介します。 半導体における拡散状態で利用するパラメータを利用します。 PDE は次に示す単純な拡散方程式になります。
dt(C) = div(D*grad(C)) ,
Cは濃度, Dは拡散率です. 拡散開始直後の濃度パラメータの値を1次元的に解析したプロットも同時に作成します。
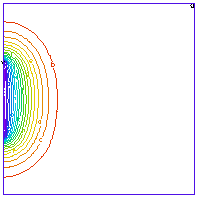
time = 1 hourにおける濃度等高線図
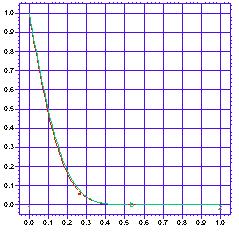
中央線上における (C/C0) の数値解と解析解の比較
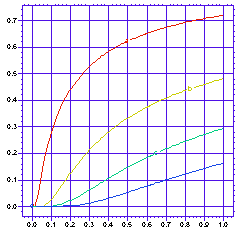
中央線上における複数ポイント点における濃度 (C/C0) と時刻の変化
