サンプルスクリプト
[10-1] 3Dバイメタルの熱応力・変形解析、
及び温度分布解析　【3d_bimetal.pde】

1. 概要

より大きな鉄板（メッシュ図の青色）に接合された、小さなアルミニウム角棒（黄色）の問題を考えます。この結合体に対して、底面の温度を100℃で固定し、側面と上面は対流によって冷却します。３Ｄの温度分布と、関連した変形、及び応力を解析します。 結合体の全ての表面は、拘束条件を与えていません。　温度分布によって自由に変形します。移動と回転をキャンセルするための積分拘束は使用しません。　３Ｄでの積分拘束は非常に高くつきますので、積分拘束は２Ｄサンプルで扱います。　その代わり、このケースでは FlexPDE が見つけた解で、作図の前に移動と回転の平均値を除去します。

2. メッシュ図

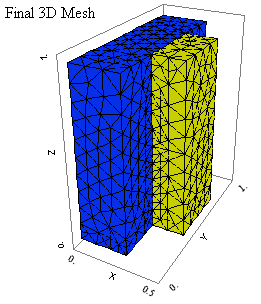
3. 解析結果

図中の {Fig.A}，{Fig.B}，{Fig.C} は、４項で対応するスクリプトを示します。

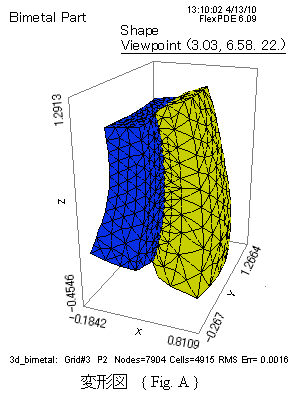
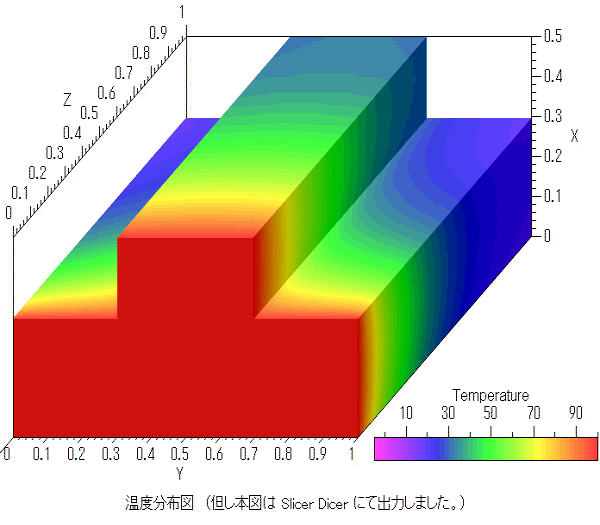
4. スクリプト

下記のスクリプトをマウスでコピーし、FlexPDE エディット･ウィンドウに貼り付けて実行する際には、日本語のコメントを除去して下さい。　そのままですと、コンパイル･エラーが発生する場合があります｡

{ 3D_BIMETAL.PDE
　３Ｄバイメタル
  This problem considers a small block of aluminum bonded to a larger block
  of iron.  The assembly is held at a fixed temperature at the bottom, and
  is convectively cooled on the sides and top.  We solve for the 3D temperature
  distribution, and the associated deformation and stress.

  All faces of the assembly are unconstrained, allowing it to grow as the
  temperature distribution demands.  We do not use an integral constraint
  to cancel translation and rotation, as we have done in 2D samples,
  because in 3D this is very expensive.  Instead, we let FlexPDE find a solution,
  and then remove the mean translation and rotation before plotting.
}

title 'Bimetal Part'

coordinates
    cartesian3

select
    painted             { show color-filled contours　等高線図を色分けで塗りつぶします。}

variables
    Tp                  { temperature 　温度 }
    U                   { X displacement 　Ｘ方向変位 }
    V                   { Y displacement 　Ｙ方向変位 }
    W                   { Z displacement 　Ｚ方向変位 }

definitions
    long = 1
    wide = 0.3
    high = 1
    tabx = 0.2
    taby = 0.4

    K                  { thermal conductivity 　熱伝達率 }
    E                  { Youngs modulus 　ヤング率 }
    alpha              { expansion coefficient 　熱膨張係数 }
    nu                 { Poisson's Ratio 　ポアソン比 }

    Q = 0              { Thermal source 　熱源 }
    Ta = 0.            { define the ambient thermal sink temperature 　周囲の熱シンク温度 }

    { define the constitutive relations 　構成関係の定義 }
    G = E/((1+nu)*(1-2*nu))
    C11 = G*(1-nu)
    C12 = G*nu
    C13 = G*nu
    C22 = G*(1-nu)
    C23 = G*nu
    C33 = G*(1-nu)
    C44 = G*(1-2*nu)/2
    b = G*alpha*(1+nu)

    { Strains 　歪み }
    ex = dx(U)
    ey = dy(V)
    ez = dz(W)
    gxy = dy(U) + dx(V)
    gyz = dz(V) + dy(W)
    gzx = dx(W) + dz(U)

    { Stresses 　応力 }
    Sx  =  C11*ex + C12*ey + C13*ez - b*Tp
    Sy  =  C12*ex + C22*ey + C23*ez - b*Tp
    Sz  =  C13*ex + C23*ey + C33*ez - b*Tp
    Txy =  C44*gxy
    Tyz =  C44*gyz
    Tzx =  C44*gzx

    { find mean translation and rotation 　移動と回転の平均値 }
    Vol = Integral(1)
    Tx = integral(U)/Vol                    { X-motion }
    Ty = integral(V)/Vol                    { Y-motion }
    Tz = integral(W)/Vol                    { Z-motion }
    Rz = 0.5*integral(dx(V) - dy(U))/Vol    { Z-rotation }
    Rx = 0.5*integral(dy(W) - dz(V))/Vol    { X-rotation }
    Ry = 0.5*integral(dz(U) - dx(W))/Vol    { Y-rotation }

    { displacements with translation and rotation removed 　移動と回転を除去した変位量 }
    { This is necessary only if all boundaries are free 　全ての境界条件がフリーの時だけに必要です }
    Up = U - Tx + Rz*y - Ry*z
    Vp = V - Ty + Rx*z - Rz*x
    Wp = W - Tz + Ry*x - Rx*y

    { scaling factors for displacement plots　変形図を作図するための縮小／拡大率 }
    Mx = 0.2*globalmax(magnitude(y,z))/globalmax(magnitude(Vp,Wp))
    My = 0.2*globalmax(magnitude(x,z))/globalmax(magnitude(Up,Wp))
    Mz = 0.2*globalmax(magnitude(x,y))/globalmax(magnitude(Up,Vp))
    Mt = 0.4*globalmax(magnitude(x,y,z))/globalmax(magnitude(Up,Vp,Wp))

initial values
    Tp = 5.
    U = 1.e-5
    V = 1.e-5
    W = 1.e-5

equations
    Tp: div(k*grad(Tp)) + Q = 0.         { the heat equation 　熱方程式 }
    U:  dx(Sx) + dy(Txy) + dz(Tzx) = 0   { the U-displacement equation 　Ｘ方向変位の方程式 }
    V:  dx(Txy) + dy(Sy) + dz(Tyz) = 0   { the V-displacement equation }
    W:  dx(Tzx) + dy(Tyz) + dz(Sz) = 0   { the W-displacement equation }

extrusion z = 0,long

boundaries
    surface 1 value(Tp)=100             { fixed temp bottom 　底部の固定温度 }
    surface 2 natural(Tp)=0.01*(Ta-Tp)  { poor convective cooling top 　上面の対流冷却 }

    Region 1    { Iron 　鉄 }
       K = 0.11
       E = 20e11
       nu  =0.28
       alpha =  1.7e-6
       start(0,0)
         natural(Tp) = 0.1*(Ta-Tp)   { better convective cooling on vertical sides　垂直側面の対流冷却 }
         line to (wide,0)
           to (wide,(high-taby)/2)
           to (wide+tabx,(high-taby)/2)
           to (wide+tabx,(high+taby)/2)
           to (wide,(high+taby)/2)
           to (wide,high)
           to (0,high)
           to close

     Region 2   { Aluminum　アルミニウム }
       K = 0.5
       E = 6e11
       nu  =0.25
       alpha =  2*(2.6e-6)              { Exaggerate expansion　誇張した熱膨張係数 }
       start(wide,(high-taby)/2)
         line to (wide+tabx,(high-taby)/2)
           to (wide+tabx,(high+taby)/2)
           to (wide,(high+taby)/2)
           to close

monitors
    contour(Tp) on y=high/2  as "Temperature"
    contour(Up) on y=high/2 as "X-displacement"
    contour(Vp) on x=4*wide/5 as "Y-displacement"
    contour(Wp) on y=high/2 as "Z-displacement"
    grid(x+My*Up,z+My*Wp) on y=high/2 as "XZ Shape"
    grid(y+Mx*Vp,z+Mx*Wp) on x=wide/2 as "YZ Shape"
    grid(x+Mz*Up,y+Mz*Vp) on z=long/4 as "XY Shape"
    grid(x+Mt*Up,y+Mt*Vp,z+Mt*Wp)  as "Shape"

plots
	cdf(Tp)
    contour(Tp) on y=high/2  as "XZ Temperature"
    contour(Up) on y=high/2 as "X-displacement"
    contour(Vp) on x=4*wide/5 as "Y-displacement"
    contour(Wp) on y=high/2 as "Z-displacement"
    grid(x+My*Up,z+My*Wp) on y=high/2 as "XZ Shape"
    grid(y+Mx*Vp,z+Mx*Wp) on x=4*wide/5 as "YZ Shape"
    grid(x+Mz*Up,y+Mz*Vp) on z=long/4 as "XY Shape"
    grid(x+Mt*Up,y+Mt*Vp,z+Mt*Wp)  as "Shape"		{ Fig. A を出力 }
    contour(Sx) on y=high/2 as "X-stress"		{ Fig. B を出力 }
    contour(Sy) on y=high/2 as "Y-stress"
    contour(Sz) on y=high/2 as "Z-stress"		{ Fig. C を出力 }
    contour(Txy) on y=high/2 as "XY Shear stress"
    contour(Tyz) on y=high/2 as "YZ Shear stress"
    contour(Tzx) on y=high/2 as "ZX Shear stress"

end