サンプルスクリプト
[10-2]平板の変形解析【Free_Plate.pde】

1. 概要

全面に等分布荷重を受ける長方形（8 x 11.2インチ）の薄板の変形を解析します｡
変位が微小な場合、たわみ U は平板たわみの重調和方程式で記述できます。
	del2(del2(U)) + Q/D = 0		del2：ラプラシアン、ラプラス演算子
ここで、Q：分布荷重　[ 14.7 ]
	D = E*h^3/(12*(1-nu^2))
	E：ヤング率（縦弾性係数）　[ 29e6 ]
	nu：ポアソン比　[ 0.3 ]
	h：板厚　[ 0.0598 ]

長方形薄板の周囲を単純支持とします。　境界条件としては、U = 0，Mn = 0 となります。
	U：荷重方向のたわみ
	Mn：薄板の曲率に関係する曲げモーメントの接線成分
後者の境界条件は、次のように近似できます。　del2(U) = 0
FlexPDEは４次の方程式を直接解くことが出来ません。
しかし、V = del2(U) と定義すれば、たわみ方程式は、次のように記述できます。
	del2(U) = V
	del2(V) + Q/D = 0
境界条件：U = 0，V = 0

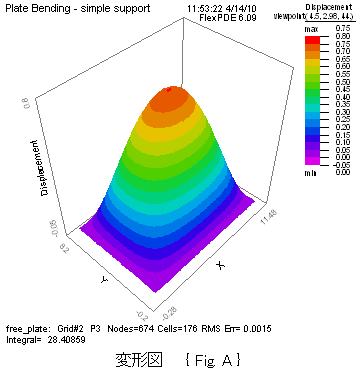
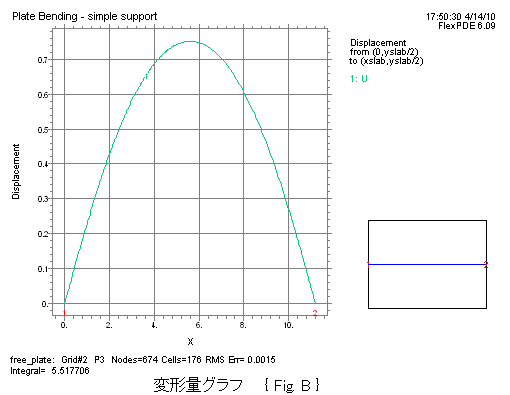
このサンプルでは、大気圧下の真空容器カバーとして、8 x 11.2インチの16ゲージ鋼板を想定します｡
この問題の解は、書籍 Roark's Formulas for Stress & Strain の例題から簡単に入手できます
(最大たわみ：Umax= 0.746)。　FlexPDE の結果は 0.750 です。

［注］これらの式を、もっと複雑な問題に拡張して適用する場合は、十分注意して下さい。　特に、方程式 del2(U) = V において、VはUに対する境界値方程式で、源になっています。　Uに境界条件値を与えることは、V = del2(U) を実行しません。
例えば、長方形薄板の周囲を単純支持から完全固定にしたい場合、上記の境界条件を適用できません。

2. メッシュ図

3. 解析結果

図中の {Fig.A}，{Fig.B}は、４項で対応するスクリプトを示します。

4. スクリプト

下記のスクリプトをマウスでコピーし、FlexPDEエディット･ウィンドウに貼り付けて実行する際には、日本語のコメントを除去して下さい。　そのままですと、コンパイル･エラーが発生する場合があります｡

{ FREE_PLATE.PDE

  This example considers the bending of a thin rectangular plate under a
  distributed transverse load.

  For small displacements, the deflection U is described by the Biharmonic
  equation of plate flexure
        del2(del2(U)) + Q/D  =  0
  where
        Q is the load distribution,
        D = E*h^3/(12*(1-nu^2))
        E is Young's Modulus
        nu is Poisson's ratio
  and   h is the plate thickness.

  The boundary conditions to be imposed depend on the way in which the
  plate is mounted.  Here we consider the case of a simply supported
  boundary, for which the correct conditions are
        U = 0
        Mn = 0
  where Mn is the tangential component of the bending moment, which in turn
  is related to the curvature of the plate. An approximation to the second
  boundary condition is then
        del2(U) = 0.

  FlexPDE cannot directly solve the fourth order equation, but if we
  define V = del2(U), then the deflection equation becomes
        del2(U) = V
        del2(V) + Q = 0
  with the boundary conditions
        U = 0
        V = 0.

  The particular problem addressed here is a plate of 16-gauge steel,
  8 x 11.2 inches, covering a vacuum chamber, with atmospheric pressure
  loading the plate.  The edges are simply supported.  Solutions to this
  problem are readily available, for example in Roark's Formulas for Stress
  & Strain, from which the maximum deflection is Umax =  0.746, as compared
  with the FlexPDE result of 0.750.

  (See FIXED_PLATE.PDE for the solution with a clamped edge.)

  Note: Care must be exercised when extending this formulation to more complex
    problems.  In particular, in the equation del2(U) = V, V acts as a source
    in the boundary-value equation for U.  Imposing a value boundary condition
    on U does not enforce V = del2(U).
}

Title " Plate Bending - simple support "

Select
    ngrid=10                    { increase initial gridding }
    cubic           { Use Cubic Basis }

Variables
     U(0.1)
     V(0.1)

Definitions
    xslab = 11.2
    yslab = 8
    h = 0.0598  {16 ga}
    L = 1.0e6
    E = 29e6
    Q = 14.7
    nu = .3
    D = E*h^3/(12*(1-nu^2))

Initial Values
    U =  0
    V =  0

Equations
     U: del2(U) = V
     V: del2(V) = Q/D

Boundaries
    Region 1
      start (0,0)
      value(U) = 0
      value(V) = 0
      line to (xslab,0)
           to (xslab,yslab)
           to (0,yslab)
           to close

Monitors
    contour(U)

Plots
    contour (U)  as "Displacement"
    elevation(U) from (0,yslab/2) to (xslab,yslab/2) as "Displacement"	{ Fig. B }
    surface(U) as "Displacement"		{ Fig. A }

End