サンプルスクリプト
[7-1] レーザーの熱流解析 【Laser_Heaflow.pde】
1. 概要
この問題は、複雑な熱流問題への適用を示します。レーザーロッドは、銅のシリンダー内部に接着されます。製造誤差でロッドは接着剤の内部へ移動します。そして、ロッドまわりの接着剤層が不均一になります。
接着剤は断熱材(熱伝導率=0.0019)で、ロッドからの放熱を妨げます。
銅のシリンダーは、その外表面の60度の角度範囲だけで、冷やされます。
レーザーロッドは、温度に依存した熱伝導率を持ちます。
我々は、レーザーロッドの温度分布を把握したいです。
熱流方程式は div(K*grad(Temp)) + Source = 0.
シリンダーの横断面をモデル化します。
これが円筒形の構造であると同時に、横断面は、暗黙の回転が直交座標平面内なので、方程式は直交座標系です。
半径2mmのロッド内部に、200(W/cc)の熱源があります。
ロッドの熱伝導率:39.8/(300+temp) (W/cm/K),temp:温度
-- この問題は、Luis Zapataによって提出されました。
2. メッシュ図
{Fig.A}~{Fig.E} は、4項で対応するスクリプトを示します。
図示でX,Y軸の単位はcmです。
{Fig.A} に解析領域の全体メッシュ図を示します。
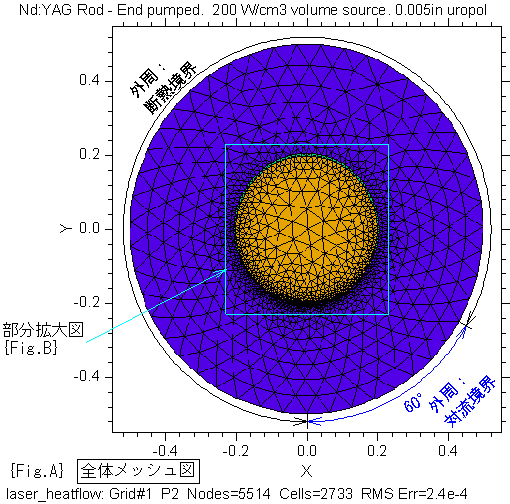
{Fig.A} で
明るい茶色部分:ロッド(半径2mm) 熱伝導率:39.8/(300+temp) (W/cm/K),temp:温度
緑色部分 :接着剤層(厚さ 0.05±0.025mm) 熱伝導率=0.0019
青紫色部分 :銅(半径5mm) 熱伝導率=3.0
空色枠線部分を拡大して {Fig.B} に示します。ロッドが下方に偏って、接着剤層が上側で厚く、下側で薄くモデル化されていることが分かります。
3. 解析結果
温度分布の全体図を{Fig.C}、部分拡大図を{Fig.D}、熱流のベクトル図を{Fig.E} に示します。
接着剤層の内側と外側で、温度に大きな差が生じています(断熱効果)。
熱流ベクトルの向きが、等温線と直交しています。
断熱境界に沿っては平行で、下側の対流(冷却)境界に対しては垂直な流れが表現されています。
メッシュ精度の問題から完全な平行、垂直ではない部分もあります。
4. スクリプト
下記のスクリプトをマウスでコピーし、FlexPDE エディット・ウィンドウに貼り付けて実行する際は、日本語のコメントを除去して下さい。そのままですと、コンパイル・エラーが発生する場合があります。
{ LASER_HEATFLOW.PDE
This problem shows a complex heatflow application.
A rod laser is glued inside a cylinder of copper.
Manufacturing errors allow the rod to move inside the glue, leaving a non-uniform glue layer around
the rod.
The glue is an insulator, and traps heat in the rod. The copper cylinder is cooled only on a
60-degree portion of its outer surface.
The laser rod has a temperature-dependent conductivity.
We wish to find the temperature distribution in the laser rod.
The heat flow equation is
div(K*grad(Temp)) + Source = 0.
We will model a cross-section of the cylinder. While this is a cylindrical structure, in cross-section
there is no implied rotation out of the cartesian plane, so the equations are cartesian.
-- Submitted by Luis Zapata
}
title "Nd:YAG Rod - End pumped. 200 W/cm3 volume source. 0.005in uropol"
Variables
temp { declare "temp" to be the system variable }
definitions
k = 3 { declare the conductivity parameter for later use 熱伝導率デフォルト値 }
krod=39.8/(300+temp){ Nonlinear conductivity in the rod.(W/cm/K) ロッドの温度依存性熱伝導
率 }
Rod=0.2 { cm Rod radius ロッドの半径 cm }
Qheat=200 { W/cc, heat source in the rod ロッド内の熱源 }
kuropol=.0019 { Uropol conductivity 接着剤層の熱伝導率 }
Qu=0 { Volumetric source in the Uropol 接着剤層内の熱源 }
Ur=0.005 { Uropol annulus thickness in r dim 接着剤層の厚さ cm }
kcopper=3.0 { Copper conductivity 銅の熱伝導率 }
Rcu=0.5 { Copper convection surface radius 銅の外周半径 cm }
tcoolant=0. { Edge coolant temperature 冷却部の温度 }
ASE=0. { ASE heat/area to apply to edge, heat bar or mount }
source=0
initial values
temp = 50 { estimate solution for quicker convergence 温度初期値:すばやい収束のため
の推定解 }
equations { define the heatflow equation 熱流方程式 }
temp : div(k*grad(temp)) + source = 0;
boundaries
region 1 { the outer boundary defines the copper region 銅の外周境界 }
k = kcopper
start (0,-Rcu)
natural(temp) = -2 * temp {convection boundary 対流境界 }
arc(center=0,0) angle 60
natural(temp) = 0 {insulated boundary 断熱境界 }
arc(center=0,0) angle 300
arc(center=0,0) to close
region 2
{ next, overlay the Uropol in a central cylinder 円筒の中心に接着剤層を重ねて定義し
ます→region 1 に上書き }
k = kuropol
start (0,-Rod-Ur) arc(center=0,0) angle 360
region 3 { next, overlay the rod on a shifted center 中心を -Ur/2 だけずらしてロッドを重ねて定義
します→上書き }
k = krod
Source = Qheat
start (0,-Rod-Ur/2) arc(center=0,-Ur/2) angle 360
monitors
grid(x,y) zoom(-8*Ur, -(Rod+8*Ur),16*Ur,16*Ur)
contour(temp)
plots
grid(x,y) {Fig.A}
grid(x,y) zoom(-(Rod+0.03),-(Rod+0.03),2*(Rod+0.03),2*(Rod+0.03)) {Fig.B}
contour (temp) painted {Fig.C}
contour(temp) zoom(-(Rod+0.03),-(Rod+0.03),2*(Rod+0.03),2*(Rod+0.03)) painted
{Fig.D}
contour(temp) zoom(-(Rod+Ur)/4,-(Rod+Ur),(Rod+Ur)/2,(Rod+Ur)/2) painted
vector(-k*dx(temp),-k*dy(temp)) as "heat flow" {Fig.E}
surface(temp)
end


