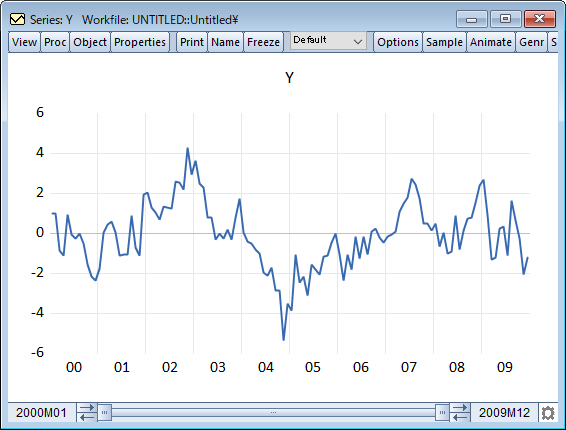
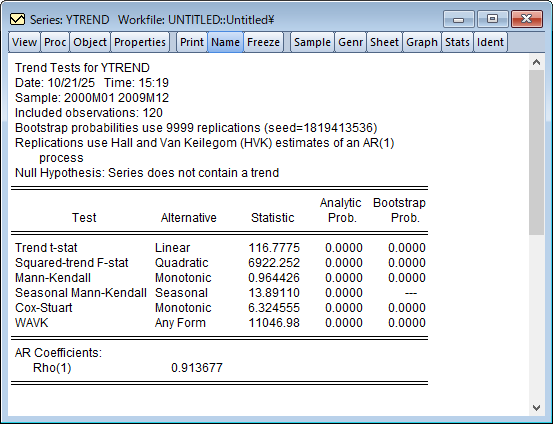
多くの経済時系列は時間的なトレンドに従います。トレンドの存在を特定することは、本質的な関心事としても、また更なる計量分析のための準備段階としても重要です。近年、トレンドの存在を検定するノンパラメトリック検定が開発されました。一般的に、これらのノンパラメトリック検定は、真のモデルに関する仮定が少なく、小さなサンプルサイズに対しても頑健です。
- EViewsでは次の検定が利用できます。$t$検定と$F$検定はパラメトリックな検定です。
- 線形トレンドの$t$検定
- 二次トレンドの$F$検定
- 単調トレンドのMann-Kendall検定
- 単調トレンドのCox-Stuart検定
- WAVK検定
線形トレンドの$t$検定
- 線形トレンドのt検定は帰無仮説:トレンドがない、対立仮設:線形トレンドがある、とし次を定義します。
\[
y_{t} = \alpha + \beta t + \epsilon_{t}
\]
$y$が検定対象の系列、$t$はトレンド項、$\epsilon_{t}$は誤差項です。これを最小二乗法で推定し、$\beta = 0$を$t$検定し、$y$とトレンド項の間の線形関係を確認します。
二次トレンドの$F$検定
- 二次トレンド検定は帰無仮説:二次トレンドがない、対立仮設:トレンドがある、として次を定義します
\[
y_{t} = \alpha + \beta t + \gamma t^{2} + \epsilon_{t}
\]
$y$が検定対象の系列、$t$はトレンド項、$\epsilon_{t}$は誤差項です。これを最小二乗法で推定し、$\beta = \gamma = 0$を$F$検定し、$y$とトレンド項の間の関係を確認します
Mann-Kendall検定
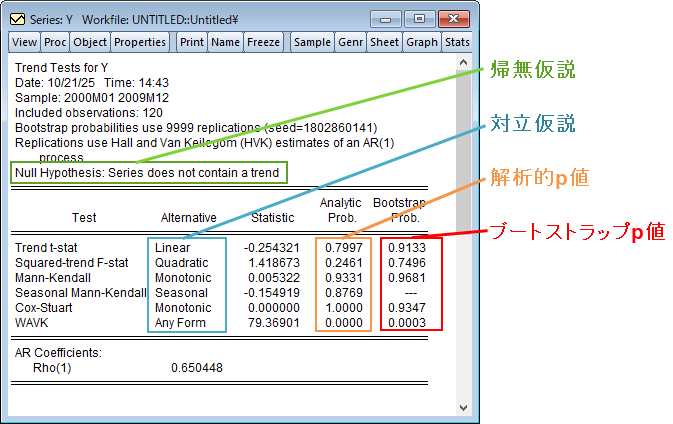
- Mann-Kendall検定は帰無仮説:単調トレンドなし、対立仮設:単調トレンドあり、を検定します。この検定はノンパラメトリックなKendallの$\tau$検定を元にしています。この検定はデータに系列相関がないことを前提としていますが、経済データの多くはこの前提を満たさないので、EViewsではブートストラップ$p$値を推定します。
Seasonal Mann-Kendall検定
- Mann-Kendall検定は帰無仮説:単調トレンドなし、対立仮設:季節性単調トレンドあり、を検定します。この検定はノンパラメトリックな、Kendallの$\tau$検定を元にしており、系列とトレンドの相関を検定しています。
これは時系列が月次または四半期頻度の場合に適用できます。データセットを月または四半期ごとに分割し、月次データの場合は12回のMK検定、四半期データの場合は4回検定を実行します。検定統計量は、個々の検定統計量の合計です。サブサンプリングを行う関係上ブートストラップ$p$値は得られません。
Cox-Stuart検定
- Cox-Stuart検定は帰無仮説:単調トレンドなし、対立仮設:単調トレンドあり、を検定します。これはWilcoxonの符号順位検定の応用であり、データの最初の3分の1の観測値と最後の3分の1の観測値をペアにして、2つのグループの中央値が等しいかどうかを検定します。具体的には、データの最初の3分の1と最後の3分の1の観測値間のペアワイズ差を計算することで検定が行われます。例えば、観測値が100個ある場合、次のように計算します。
\begin{gather}
y_{67}-y_{1} \\
y_{66}-y_{2} \\
\cdots \\
y_{99}-y_{32} \\
y_{100}-y_{33}
\end{gather}
これらの差が計算されると、正の差と負の差の数がカウントされ、検定統計量は次のように与えられます。
\[
z = \frac{S-T/6}{\sqrt{T/12}}
\]
$S$は正または負の最大差、$T$は観測数です。データに系列相関がなければ、$z$は正規分布に従い、通常通り$p$値を計算できます。Mann-Kendall検定と同じくブートストラップ推定を行います。
Wang, Akritas and Van Keilegom (WAVK)検定
- WAVK検定は、トレンドがないという帰無仮説と、一般的なトレンドがあるという対立仮説を検定するものです。WAVKは、回帰関数の適合性を判定するノンパラメトリック診断検定であり、Lyubchicha, Gel, El-Shaarawi (2013)によってトレンド検定に適用されました。WAVK検定統計量は次のように求められます。
\begin{align}
WAVK &= MST - MSE \\
MST &= \frac{k}{T-1}\sum_{t=1}^{T}(\bar{V}_{t} - \bar{V}_{..})^{2} \\
MSE &= \frac{k}{T(k-1)}\sum_{t=1}^{T}\sum_{j=1}^{k}(\bar{V}_{tj} - \bar{V}_{t})^{2}
\end{align}
$\bar{V}$は$y$の$k$期の移動平均、$\bar{V}_{..}$は$\bar{V}_{i}$の平均、$\bar{V}_{i}$は$\bar{V}$の$i$番目の要素、$\bar{V}_{ij}$は$\bar{V}$の$(i,j)$番目の要素です。さらにEViewsで実行される検定では、$k = ceil(T/10)$としています。前提条件のもとでは、WAVK統計量は次の分布に従います。
\[
(\frac{T}{k})^{1/2} WAVK \sim N(0,\frac{4}{3}\sigma^{2})
\]
$\sigma^{2}$の推定値は、
\[
\hat{\sigma}^{2} = \frac{1}{2(T-1)} \sum_{t=2}^{T} (y_{t} - y_{t-1})^{2}
\]
系列相関がないという前提が満たされない場合に備え、EViewsはブートストラップ$p$値も報告します。
ブートストラッピング
- 系列相関の影響を避けるため、seasonal Mann-Kendall検定以外ではブートストラッピングを行うことができます。トレンド検定ダイアログボックスにはNone, Ordinary, Sieve, Sieve(HVK)の4つの選択肢があります。
- None: ブートストラッピングを行わず、解析的$p$値のみを報告します。
- Ordinary: データに対して、通常のリサンプリングして、ブートストラッピングを行います
- SieveおよびSieve(HVK)はデータ内の系列相関を考慮したsieveブートストラップを実行します
sieveブートストラッピングは、系列内のデータに対する自己回帰過程を推定し、その結果を用いて推定された相関構造を保持するブートストラップ標本を生成することで、データの系列依存性を考慮します。このプロセスの「sieve(ふるい分け)」部分とは、サンプルサイズに応じて自己回帰過程の次数$p$をゆっくりと増加させ、モデルが過学習することなく依存構造を正確に捉えるアプローチを指します。
Hall and Van Keilegom (2003) (HVK)法は時系列誤差を含むノンパラメトリック回帰における誤差共分散と自己回帰パラメータの推定のための差分ベース手法です。HVK法をsieveブートストラッピングに組み込むには、HVK法を用いてAR係数と誤差を推定し、推定された係数と残差を用いてブートストラップ標本を生成する必要があります。