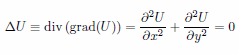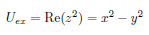Sample Scripts from GB Books
ラプラス方程式、ポアッソン方程式
ここで紹介するスクリプトはGunnar Backstrom氏の承諾のもと、書籍 “Simple Fields of Physics by Finite Element Analysis” に記されている多数のFlexPDE適用事例 の中からその一部を紹介するものです。
PDF版 (860KB)
ここでは2次元の正方形領域において変数 U(x, y) に関するラプラス方程式 |
|
(1) |
について考えることにします。実際の物理的な問題にFlexPDEを適用する前に、その計算精度を確認する意味で解析解との対比をまず行ってみましょう。良く知られているように正則な複素関数の実数部、あるいは虚数部はラプラス方程式を満足します。そこでここでは |
|
(2) |
という関数を想定し、境界上でこの関数値を指定することにします(Dirichlet型境界条件)。もちろんFlexPDEはこれが厳密解であることなど認識できるわけではないので、ひたすら有限要素法に基づき数値解を計算します。 |
1. Problem descriptor [ laplace01a.pde ]
まずタイトルを設定します。 |
2. 実行結果
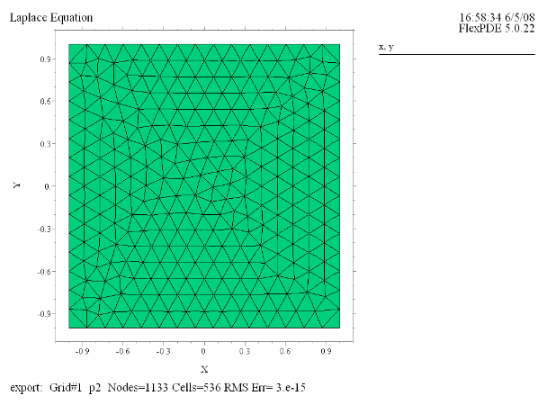
(1) Grid(x, y) |
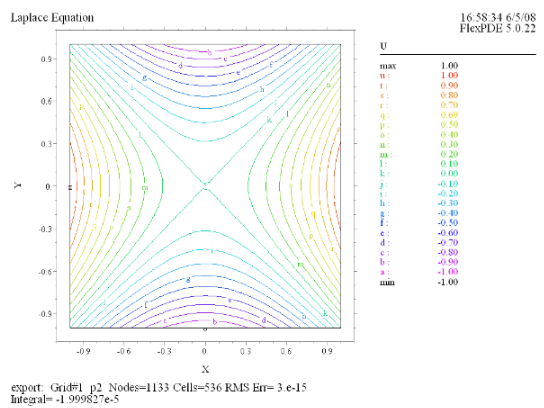
(2) Contour(U) |
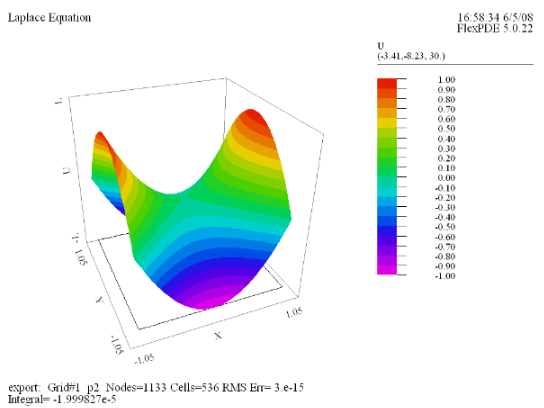
(3) Surface(U) |
(4) Contour(U_ex) |
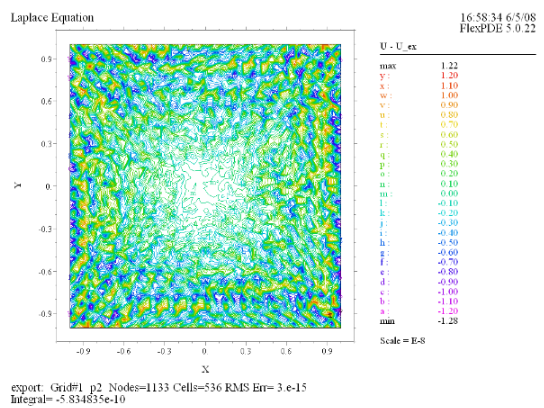
(5) Contour(U - U_ex) |
ここでは正方形領域を対象に計算結果の検証を行ったわけですが、境界の形状が円形であっても三角形であっても同様の操作で行えます。なお、境界上で値が指定されたとき、その条件を満たすラプラス方程式の解は一つに限られる点にご注意ください。 |