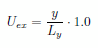Sample Scripts from GB Books
GB003: 2次元における電導
ここで紹介するスクリプトはGunnar Backstrom氏の承諾のもと、書籍 “Simple Fields of Physics by Finite Element Analysis” に記されている多数のFlexPDE適用事例 の中からその一部を紹介するものです。
PDF版 (1353KB)
GB002のケースでは金属オブジェクト全体が等電位の状態に置かれていました。しかしオブジェクトの異なる部分の間に電位がかけられた場合には電流が流れることになります。普通の金属の場合には電流密度(electrical current density)ベクトル J と電場ベクトル E、ポテンシャル U の間には次の関係が成立します。 |
|
(1) |
ここに σ は電導率(electric conductivity)を表すパラメータです。一方、連続の式から |
|
(2) |
が導かれます。ここに ρ は電荷密度を表します。定常状態ではこの第2項が0となるため、(1)と(2)を結合することにより |
|
(3) |
というラプラス型の偏微分方程式が導かれます。ただし σ は空間的に変化する可能性があるため括弧の外に出すことはできません。しかしこのような場合でもFlexPDEでの扱いは容易です。なお、FlexPDEに対し方程式を定義する際、従属変数 U を明示的に含んだ(3)の形の数式を入力する必要はありません。div(J) = 0 と記述するだけで(1)により U に関する2階の偏微分方程式が自動的に誘導されます。この U に関する解から E や J が算出されることになります。 |
1. 矩形プレート中の電導
|
1.1 Problem descriptor [ econduction01a.pde ]
まずタイトルを設定します。 |
1.2 実行結果
(1) Grid(x, y) |
(2) Contour(U) |
(3) Surface(U) |
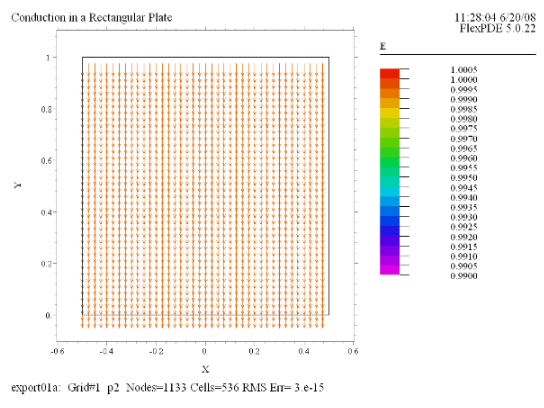
(4) Vector(E) |
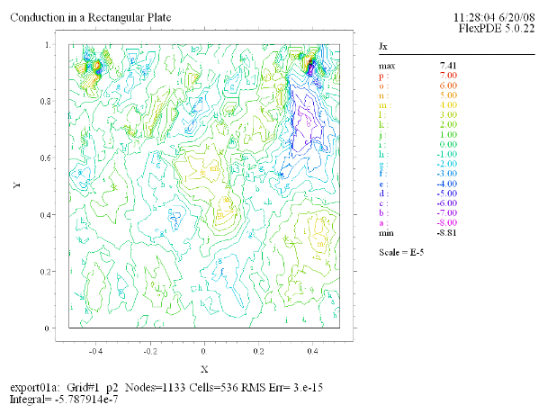
(5) Contour(Jx) |
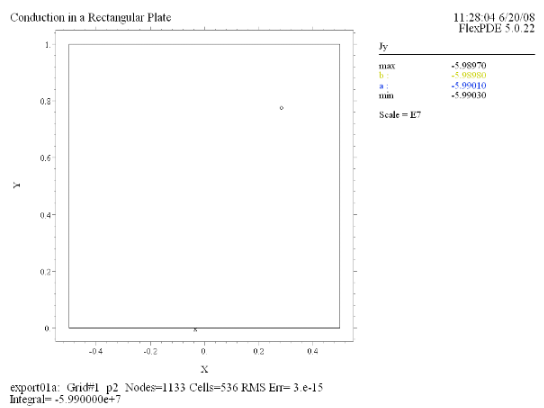
(6) Contour(Jy) |
(7) Contour(Jm) |
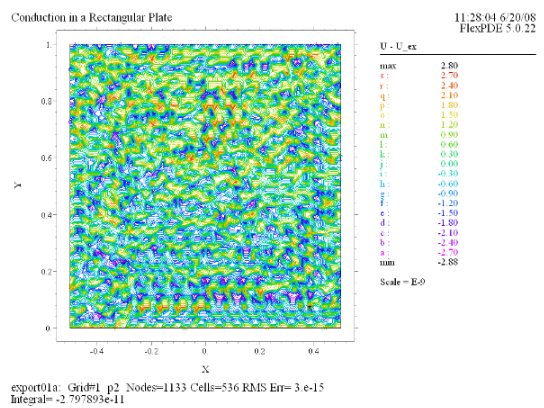
(8) Contour(U - U_ex) |

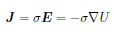
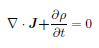
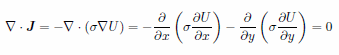
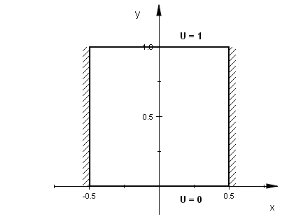 最初に最も簡単な例として右のような銅製の矩形プレートについて考えることにします。この上辺に
1.0V の電位をかけ、下辺は 0V に維持、一方、左右の境界は絶縁状態に置かれているものとします。今、下辺の位置を y = 0
におき、矩形のy方向の長さを Ly とすると U の厳密解は
最初に最も簡単な例として右のような銅製の矩形プレートについて考えることにします。この上辺に
1.0V の電位をかけ、下辺は 0V に維持、一方、左右の境界は絶縁状態に置かれているものとします。今、下辺の位置を y = 0
におき、矩形のy方向の長さを Ly とすると U の厳密解は