Sample Scripts from GB Books
GB003: 2次元における電導
2. 台形プレート中の電導
|
2.1 Problem descriptor [ econduction01b.pde ]
基本形は一つ前の econduction01a.pde と変りません。 |
2.2 実行結果
(1) Grid(x, y) |
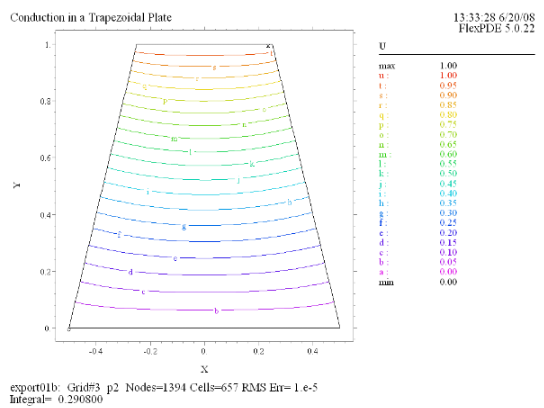
(2) Contour(U) |
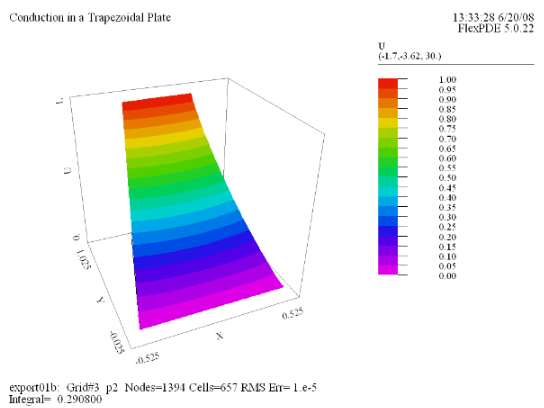
(3) Surface(U) |
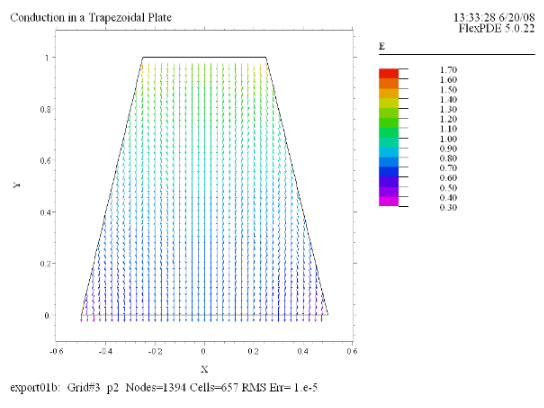
(4) Vector(E) norm |
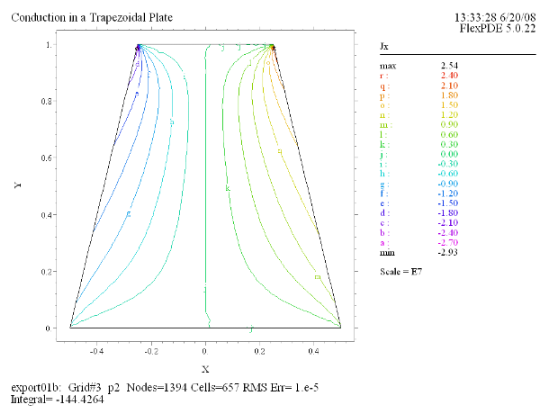
(5) Contour(Jx) |
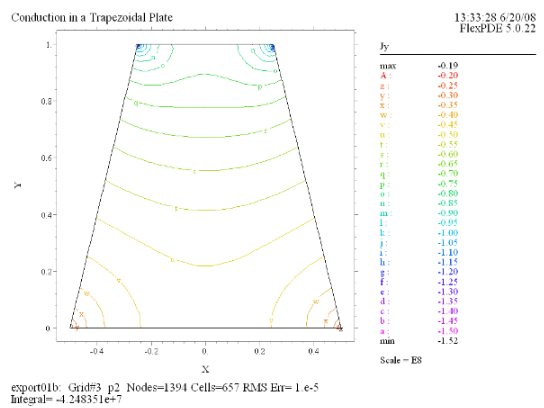
(6) Contour(Jy) |
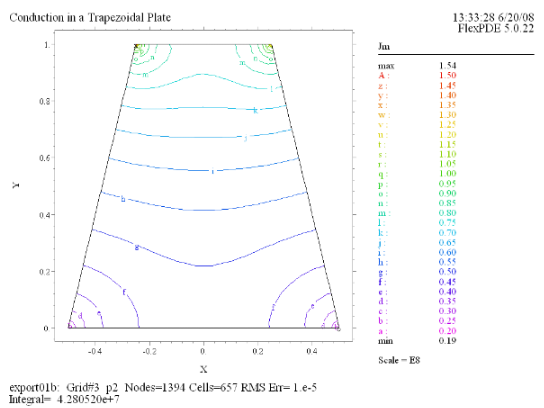
(7) Contour(Jm) |

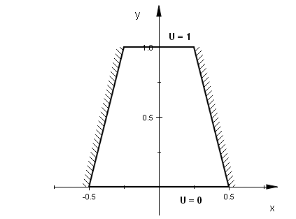 今度はプレートの形状を台形に変えて電流の流れを調べてみましょう。この場合、解析的な手法で厳密解を求めることはできないので数値解に頼らざるを得ません。境界条件は前の例と同様、上辺で
U = 1、下辺で U = 0、両側の斜辺は絶縁境界であるとします。
今度はプレートの形状を台形に変えて電流の流れを調べてみましょう。この場合、解析的な手法で厳密解を求めることはできないので数値解に頼らざるを得ません。境界条件は前の例と同様、上辺で
U = 1、下辺で U = 0、両側の斜辺は絶縁境界であるとします。