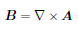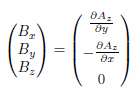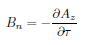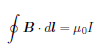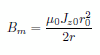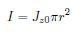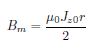Sample Scripts from GB Books
GB008: 2次元静磁場
ここで紹介するスクリプトはGunnar Backstrom氏の承諾のもと、書籍 “Simple Fields of Physics by Finite Element Analysis” に記されている多数のFlexPDE適用事例 の中からその一部を紹介するものです。
PDF版 (849KB)
マックスウェルの方程式の一つは |
|
(1) |
であるわけですが、静磁場ということでは単に |
|
(2) |
を考えれば良いことになります。ここに H は磁場の強度、J は電流密度、D は電束密度を意味します。これを直交座標系での成分で表すと次のようになります。 |
|
(3) |
今、磁場としてx成分とy成分のみを持つケースを考えることにするとJx, Jyが消えて |
|
(4) |
のみが残る形となります。一方、磁束密度を B としたとき、ベクトルポテンシャル A(x, y, z) を考えることができて |
|
(5) |
と表現できます。ただし(x, y)平面に平行なベクトル場 H と B を考えようとしているわけですから、Ax, Ay 共に0という条件が付く形となります。B = μH に配慮すると(μ は透磁率)、数式(5)から |
|
(6) |
が導かれます。このHx, Hy を数式(4)に代入すると Az に関する2階の偏微分方程式 |
|
(7) |
が導出されてきます。FlexPDEに対して指定する方程式はもちろん(7)の形でも良いのですが、DEFINITIONSセクションで(6)の関係を規定してやれば、EQUATIONSセクションで設定する方程式は(4)の形でも構いません。ポテンシャル Az が求まればベクトル場 H と B は(6)によって算出できます。 |
1. 電線周辺の磁場
この場合、電線の内外で厳密解が知られているため、FlexPDEによる計算結果との対比も行うことにします。 |
1.1 Problem descriptor [ magnetics01a.pde ]
まずタイトルを設定します。 最後に出力すべき情報を規定します。 |
1.2 実行結果
(1) Grid(x, y) |
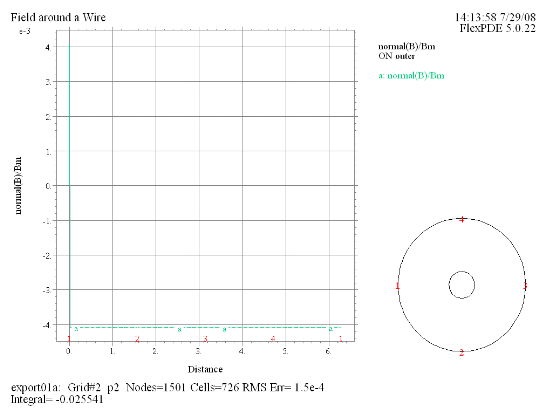
(2) Elevation(normal(B)/Bm) on 'outer' |
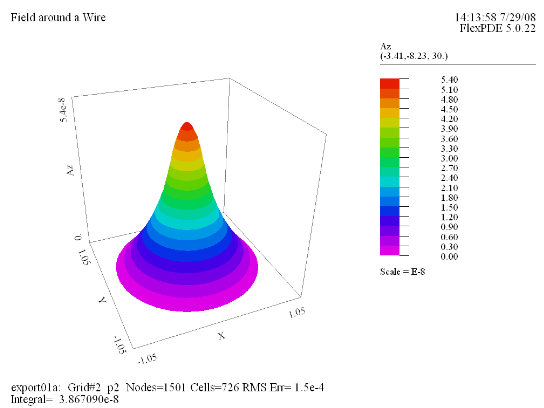
(3) Surface(Az) |
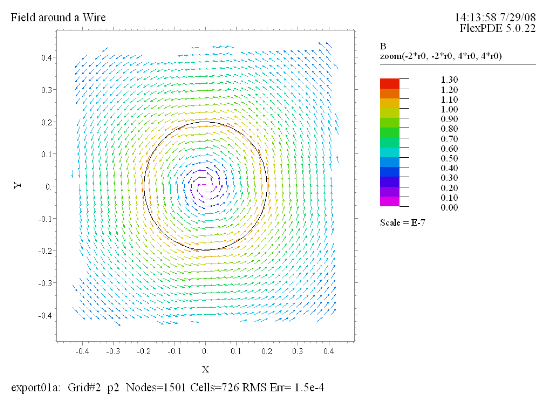
(4) Vector(B) norm zoom(-2*r0, -2*r0, 4*r0, 4*r0) |
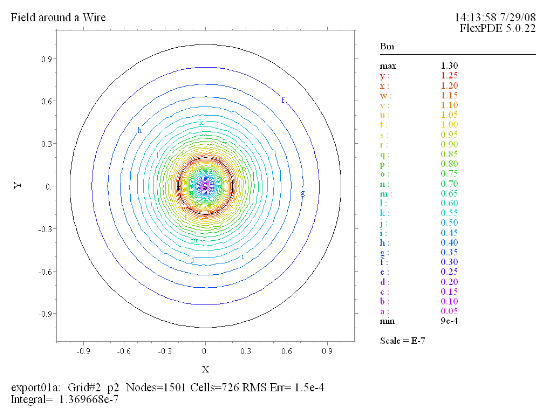
(5) Contour(Bm) |
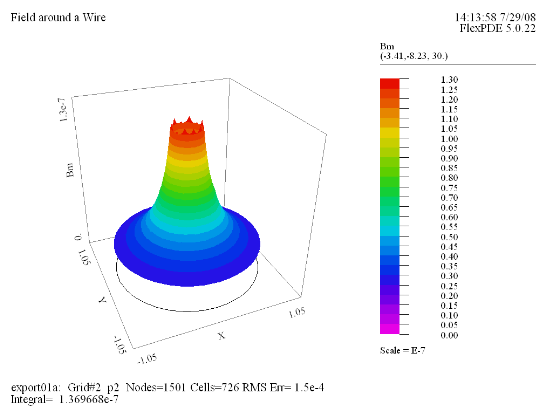
(6) Surface(Bm) |
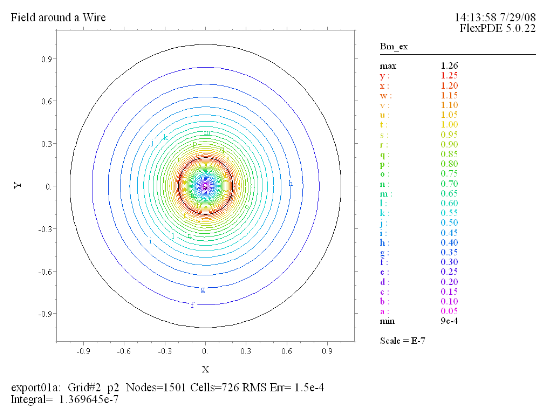
(7) Contour(Bm_ex) 厳密解は電線内外の円周上で |
|
(8) |
が厳密解を与える数式となります。一方、電線内の点に対しては |
|
(9) |
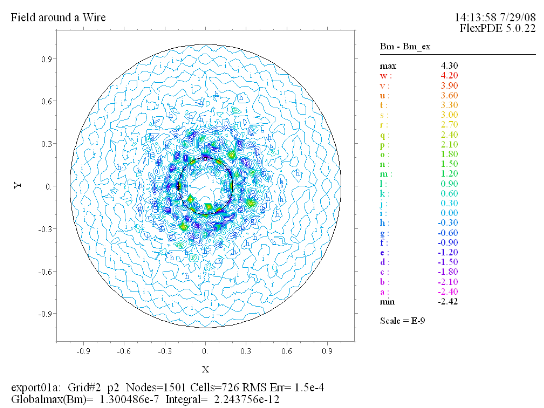
(8) Contour(Bm - Bm_ex) Report(Globalmax(Bm)) Note: SELECTセクションで指定した Errlim はポテンシャル Az に対するものである点に注意。磁束密度ベクトル B は Az に対する偏微分操作で得られるため、数値計算に伴う誤差は大きくなっても不思議ではありません。 |
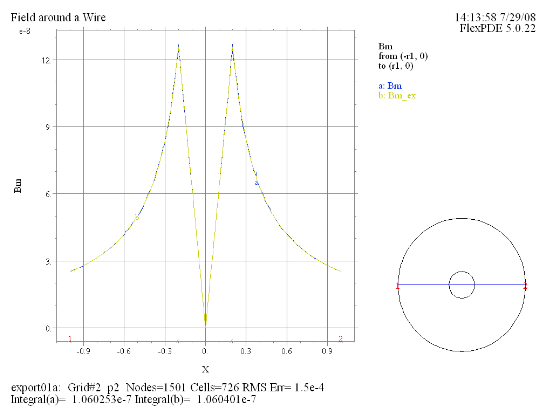
(9) Elevation(Bm, Bm_ex) from (-r1, 0) to (r1, 0) |

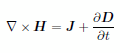
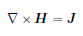
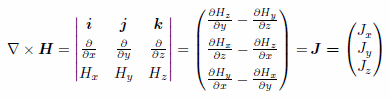
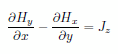
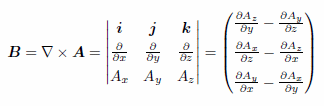
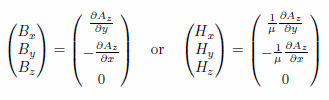
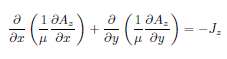
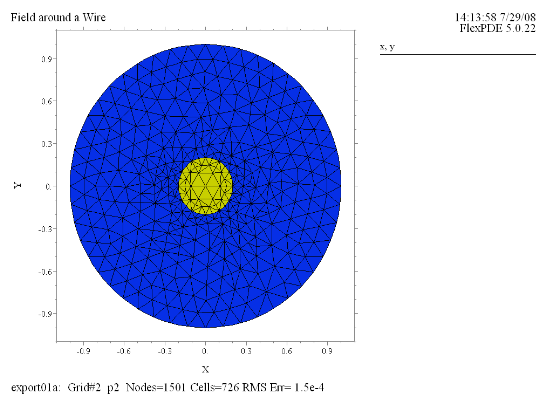
 右の図の灰色の円形は電線の垂直断面を表したものです。電流密度は一様で
Jz = 1
としたときの磁場の様子を円形のドメイン上で計算してみます。ただし電線の長さは十分に長いものとします。また透磁率としては電線周囲、電線内(銅製)、共に真空の透磁率 μ0 を使用します。
右の図の灰色の円形は電線の垂直断面を表したものです。電流密度は一様で
Jz = 1
としたときの磁場の様子を円形のドメイン上で計算してみます。ただし電線の長さは十分に長いものとします。また透磁率としては電線周囲、電線内(銅製)、共に真空の透磁率 μ0 を使用します。