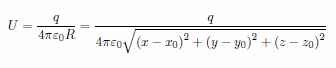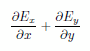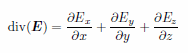Sample Scripts from GB Books
GB009: 3次元の電場
ここで紹介するスクリプトはGunnar Backstrom氏の承諾のもと、書籍 “Simple Fields of Physics by Finite Element Analysis” に記されている多数のFlexPDE適用事例 の中からその一部を紹介するものです。
PDF版 (1082KB)
FlexPDEで3次元の場を扱う場合には、x-y平面に定義されたbase planeをz軸方向に押出す(extrusion)という考え方が基本になります。 |
1. 電荷周辺の電場(2電荷の場合)
|
点 (x0, y0, z0 ) に電荷 q が置かれているときの静電ポテンシャル U を与える数式: |
|
(1) |
1.1 Problem descriptor [ 3dfields1a.pde ]
まずタイトルを設定します。 |
1.2 実行結果
(1) Grid(x, y, z) |
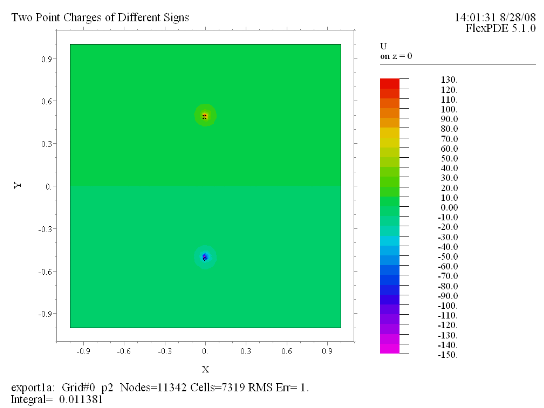
(2) Contour(U) painted on z = 0 |
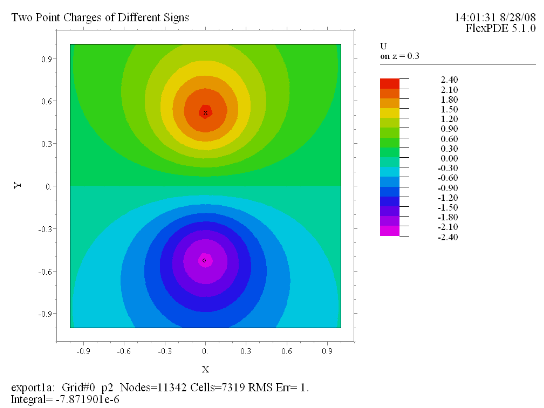
(3) Contour(U) painted on z = 0.3 |
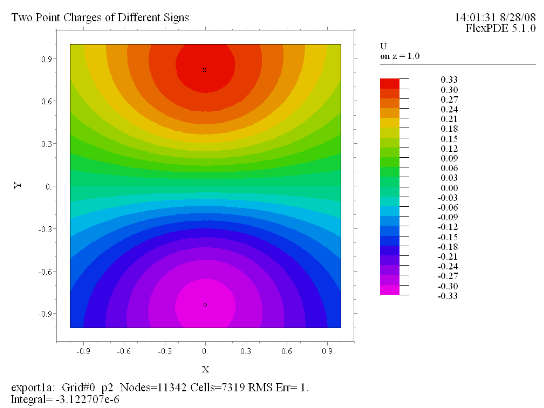
(4) Contour(U) painted on z = 1.0 |
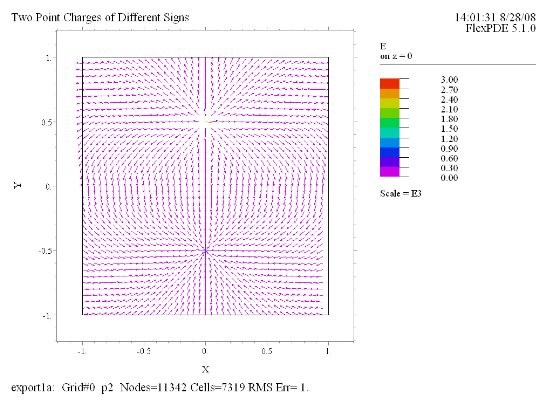
(5) Vector(E) norm on z = 0 |
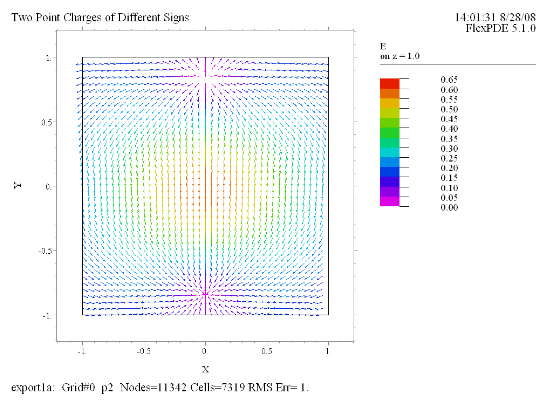
(6) Vector(E) norm on z = 1.0 |
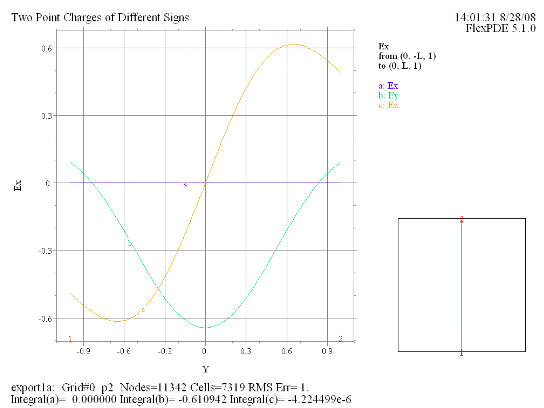
(7) Elevation(Ex, Ey, Ez) from (0, -L, 1) to (0, L, 1) |
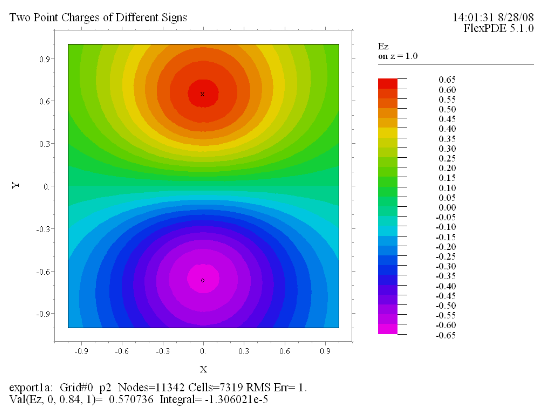
(8) Contour(Ez) painted on z = 1.0 Report(Val(Ez, 0, 0.84, 1)) |
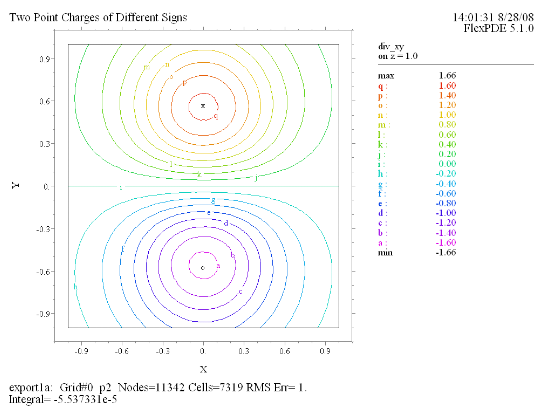
(9) Contour(div_xy) on z = 1.0 |
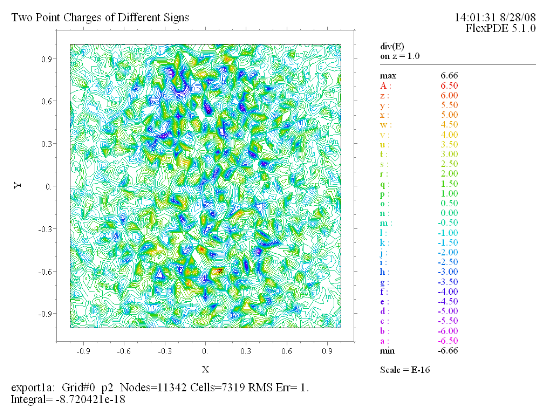
(10) Contour(div(E)) on z = 1.0 |

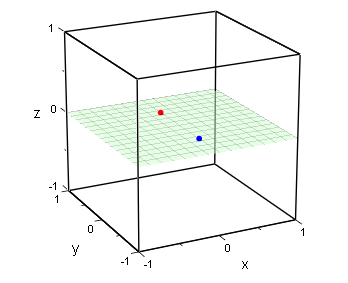 右の図は電場の様子を調べようとする
右の図は電場の様子を調べようとする