Sample Scripts from GB Books
GB010: 3次元の熱伝導
ここで紹介するスクリプトはGunnar Backstrom氏の承諾のもと、書籍 “Simple Fields of Physics by Finite Element Analysis” に記されている多数のFlexPDE適用事例 の中からその一部を紹介するものです。
PDF版 (349KB)
FlexPDEで3次元の場を扱う場合には、x-y平面に定義されたbase planeをz軸方向に押出す(extrusion)という考え方が基本になります。 |
1. 平衡状態
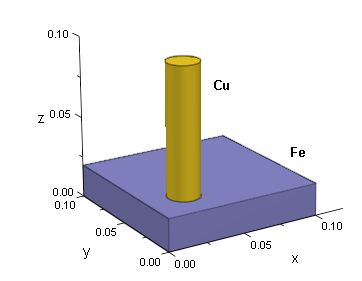
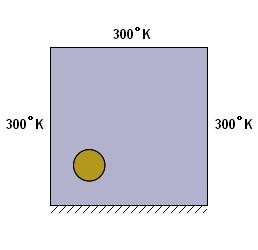
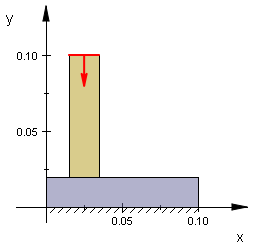
ここでは右図のような鉄の板に銅製の円柱を溶接した構造体(単位はm)を考え、 その円柱部上面に1e6の熱流束を与えたときの平衡状態における熱伝導の様子をFlexPDE を用いて解析します。ただし境界条件としては次の平面図、立面図に示したようなものを想定します。
なお、支配方程式に関する背景情報については GB004 を参照ください。
| 平面図 |
立面図 |
|---|---|
|
|
正面は熱的に絶縁されており、他は一定温度300度Kに保つものとします。 この条件はz軸方向にextrudeされた側壁に対しても適用される点に注意してください。 |
底面は熱的に絶縁状態、一方円柱部上面からは1e6の熱流束が与えられるものとします。 |
1.1 Problem descriptor [ 3dfields2a.pde ]
まずタイトルを設定します。 次に座標系が3次元直交座標系であることを明示します(デフォルトはCartesian2)。 関連するパラメータや数式を定義します。r0 は円柱の半径、中心の位置は (L/4, L/4)、z0 は鉄板の厚さを意味しています。 z軸方向へのextrusionを定義します。下から順に境界面(Surface)とそれらにはさまれた層(Layer)を規定して行きます。 最後に出力すべき情報を規定します。 |
1.2 実行結果
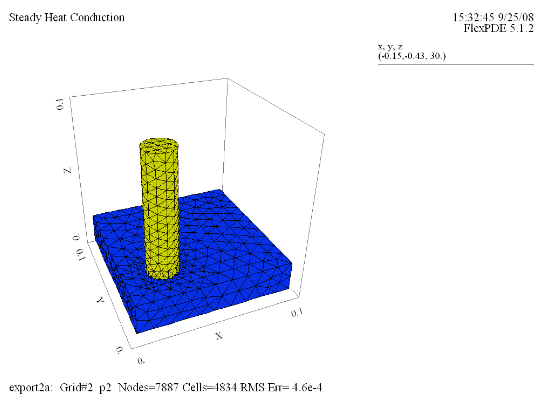
(1) Grid(x, y, z) |
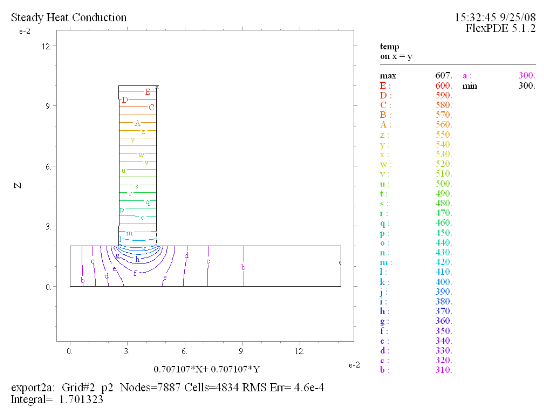
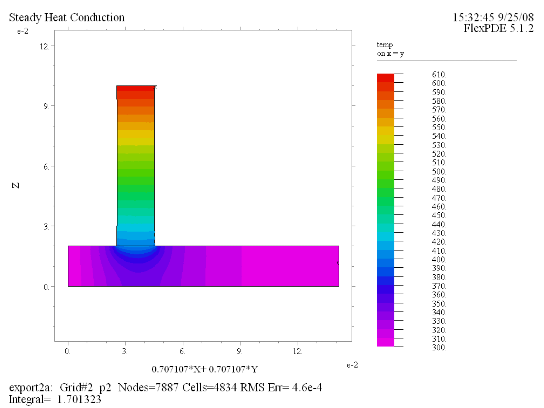
(2) Contour(temp) on x = y |
(3) Contour(temp) painted on x = y |
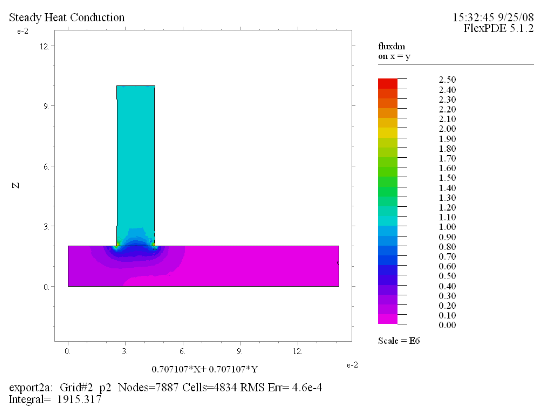
(4) Contour(fluxdm) painted on x = y |
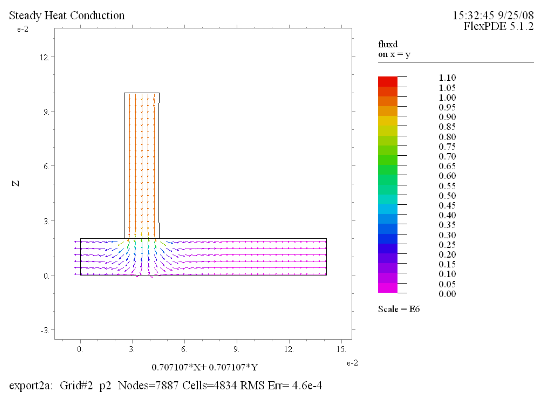
(5) Vector(fluxd) norm on x = y |
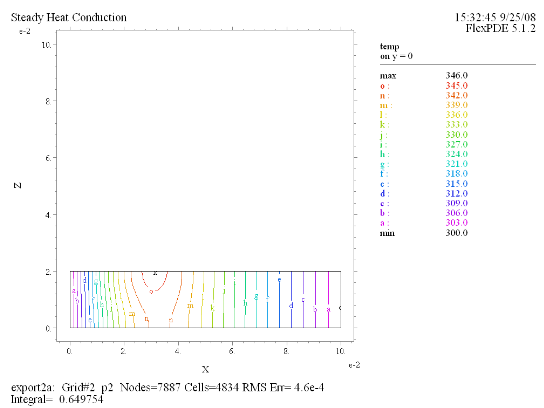
(6) Contour(temp) on y = 0 |
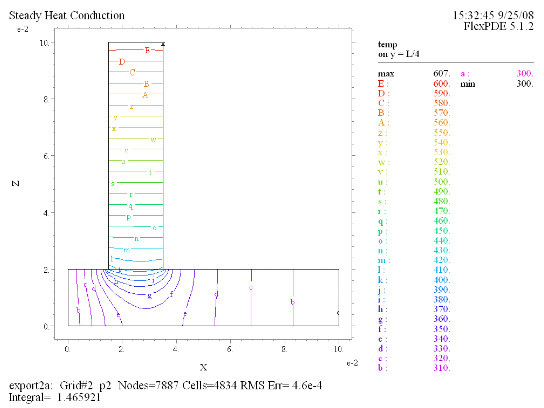
(7) Contour(temp) on y = L/4 |
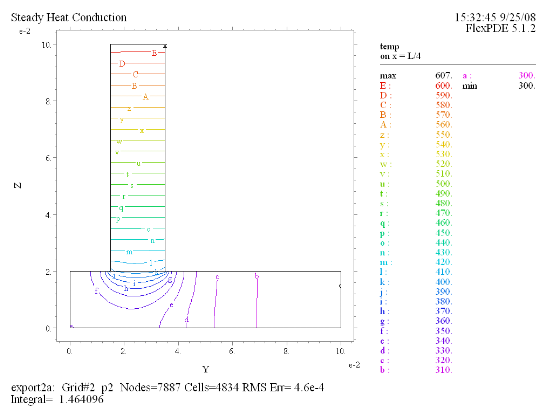
(8) Contour(temp) on x = L/4 |
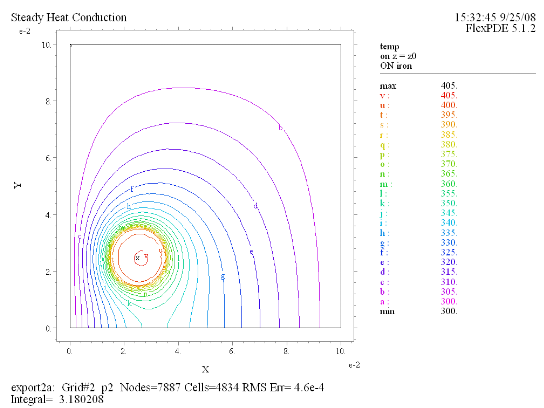
(9) Contour(temp) on z = z0 on 'iron' |
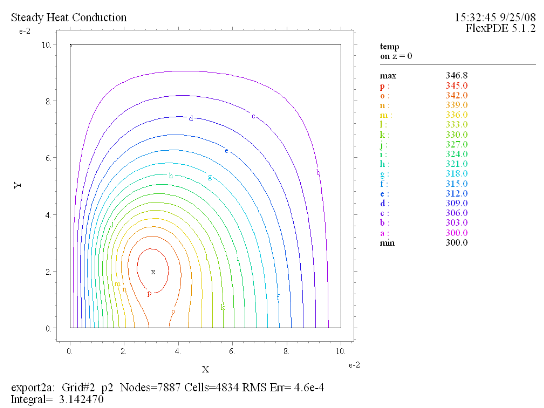
(10) Contour(temp) on z = 0 |