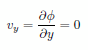Sample Scripts from GB Books
GB011: 2次元の完全流体
ここで紹介するスクリプトはGunnar Backstrom氏の承諾のもと、書籍 “Simple Fields of Physics by Finite Element Analysis” に記されている多数のFlexPDE適用事例 の中からその一部を紹介するものです。
PDF版 (672KB)
2次元における流体の流れを分析するに際し、ここでは
という理想的なケースを想定することにします。この場合には流れはポテンシャル流れとなり、速度ベクトルはスカラーのポテンシャル関数 Φ を用いて |
|
(1) |
のように表現することができます。一方、連続の式 |
|
(2) |
(ρ は密度、v は速度ベクトル)は非圧縮性流体の場合、ρ =一定となるため、 |
|
(3) |
に帰着されます。従って (1) を (3) に代入することによって次のラプラス方程式を得ることができます。 |
|
(4) |
この型の流れの場合、渦ベクトル ω のz成分を計算してみると |
|
(5) |
を使って算出することができます。ただし数式(5)では重力の働く方向を z 軸方向と仮定しています。 |
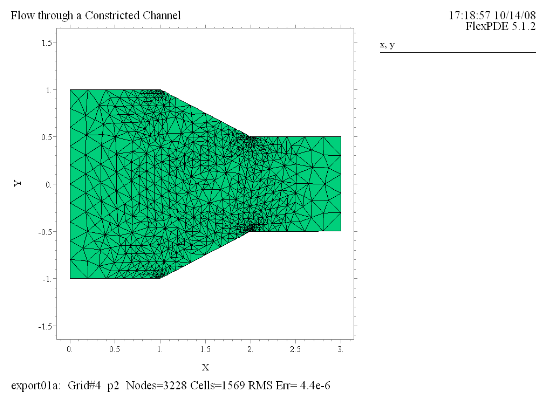
1. くびれのあるチャネルにおける流れ
方程式(4)と(5)は連立させる必要はないため、EQUATIONSセクションで指定するのは(4)のみとし、圧力 p を計算する数式はDEFINITIONSセクション中に記述するというアプローチを取ります。 境界条件としてはチャネル左端 x = 0 におけるx方向の流速 vx0 = 3.0 と圧力 p0
= 1e5 を規定します(単位はSI系)。従属変数が Φ であることから境界条件の記述の中での vx0 の指定にはNatural文が使用されることになります。一方
x = 3 におけるチャネル右端においてはValue文により Φ
= 0 という定数値を指定しています。定数値としては別に 0 でなくても良いわけですが、これによってこの境界上で |
1.1 Problem descriptor [ pfluid01a.pde ]
まずタイトルを設定します。 関連するパラメータや数式を定義します。単位としてはSI単位系を使用します。p
に関する数式は数式(5)に基づくものですが、2次元の流れなので gz の項は無視できます。div(v), curl(v)
という数式は検証用に設定しています。 最後に出力すべき情報を規定します。 |
1.2 実行結果
(1) Grid(x, y) |
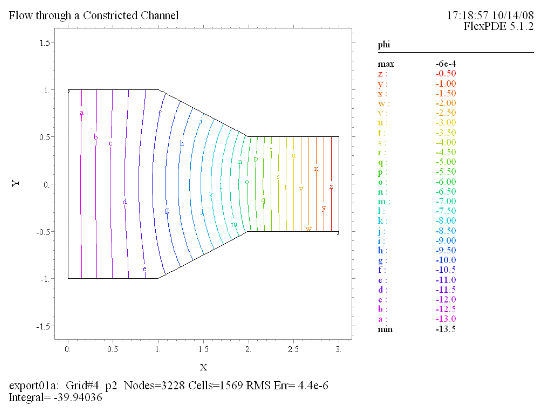
(2) Contour(phi) |
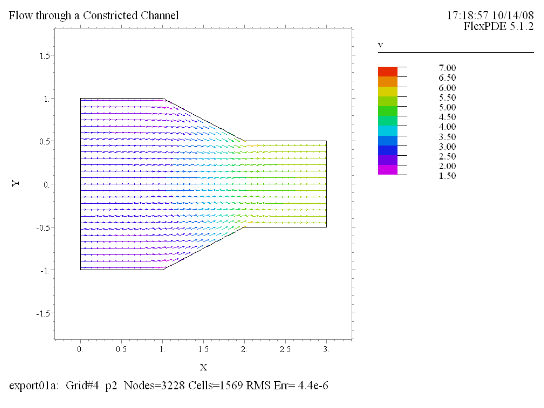
(3) Vector(v) norm |
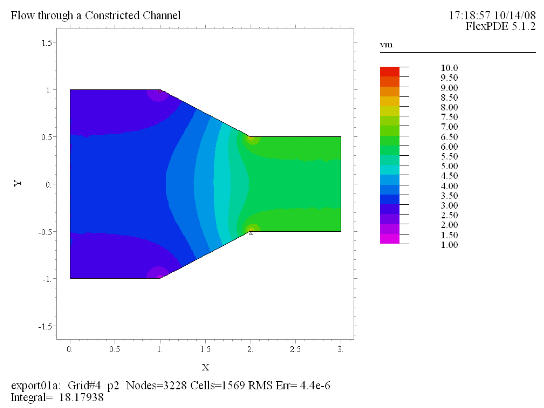
(4) Contour(vm) painted |
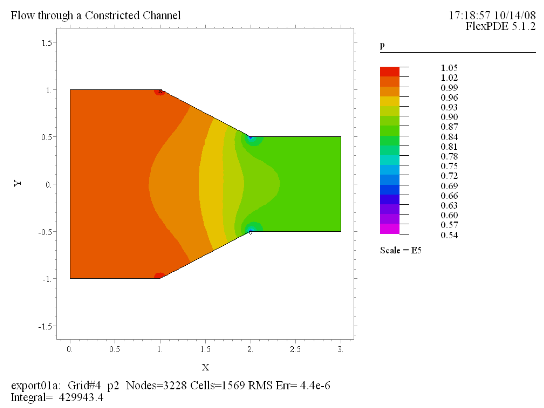
(5) Contour(p) painted |
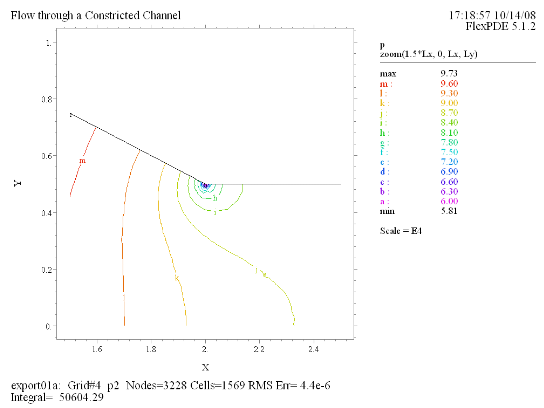
(6) Contour(p) zoom(1.5*Lx, 0, Lx, Ly) |
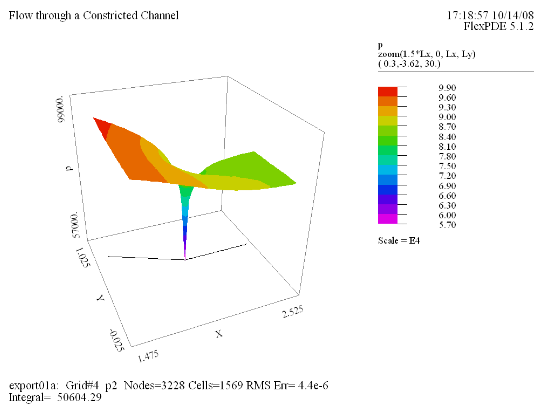
(7) Surface(p) zoom(1.5*Lx, 0, Lx, Ly) |
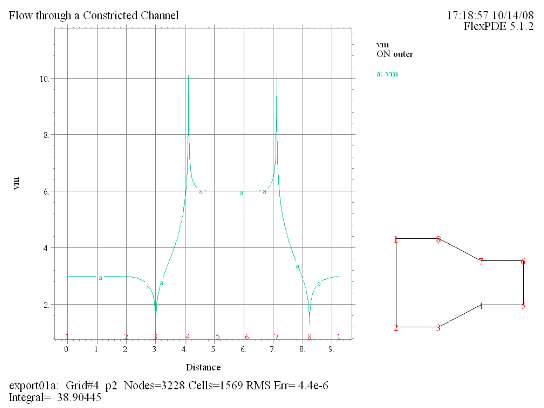
(8) Elevation(vm) on 'outer' |
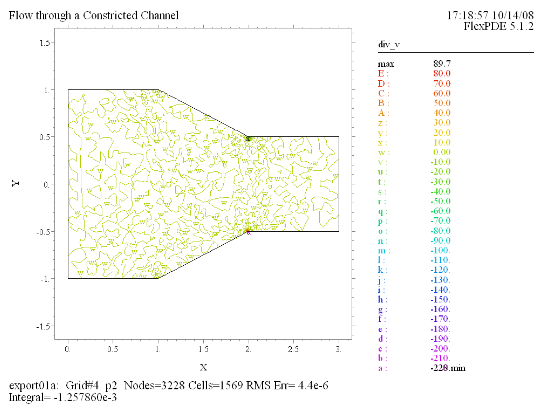
(9) Contour(div_v) |
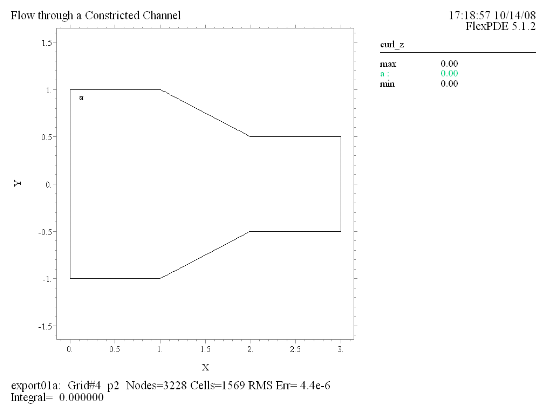
(10) Contour(curl_z) |

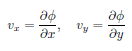
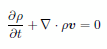
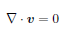
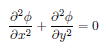
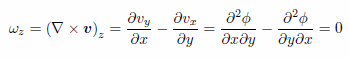
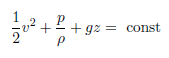
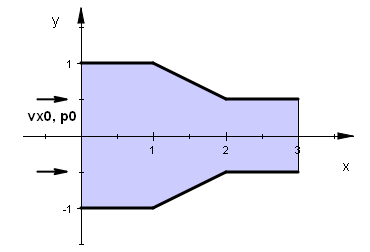 ここでは右図のよう
に先で太さが狭まったチャネルにおける水平な流れを分析します。重力の働く方向はz軸方向であり、ここで解析対象とする2次元の流れには影響が及ばないため、ベルヌーイの定理における
gz の項は無視します。
ここでは右図のよう
に先で太さが狭まったチャネルにおける水平な流れを分析します。重力の働く方向はz軸方向であり、ここで解析対象とする2次元の流れには影響が及ばないため、ベルヌーイの定理における
gz の項は無視します。