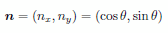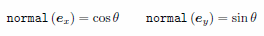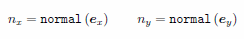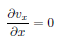Sample Scripts from GB Books
GB012: 2次元の粘性流体
3. くびれのあるチャネルにおける流れ [1]
ただし最初に発散項を含まない形(C = 0、資料 GB012a.pdf 中の数式(13)参照)での求解を試みます。結果的に誤った解が誘導されてしまう点に注意してください。 |
3.1 Problem descriptor [ vfluid01c.pde ]
まずタイトルを設定します。 従属変数を規定します。 関連するパラメータや数式を定義します。単位としてはSI単位系を使用します。 資料 GB012a.pdf 中に記載されている方程式(12),
(13)を定義します。なお、方程式(13)中の発散項については取り敢えず無視して(C = 0)計算を行ってみます。 BOUNDARIESセクションでは境界形状の規定と同時に境界条件を設定します。入口側では
p = δp, 出口側では p = 0 という指定を行っています。入口、出口部におけるNatural(vx) = 0
という指定は 最後に出力すべき情報を規定します。 |
3.2 実行結果
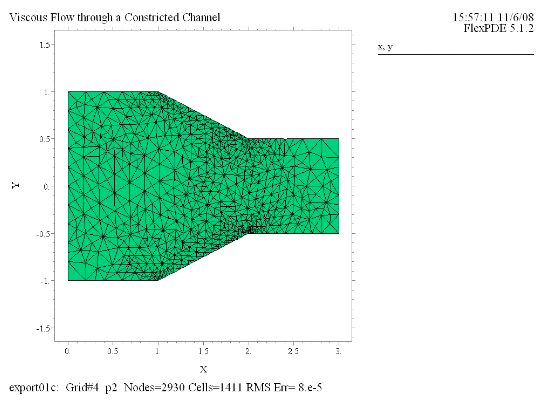
(1) Grid(x, y) |
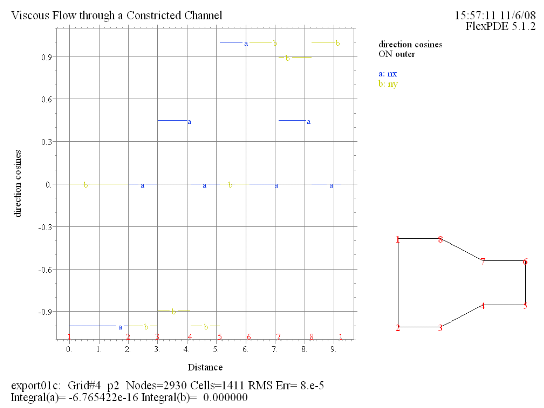
(2) Elevation(nx, ny) on 'outer' as 'direction cosines' |
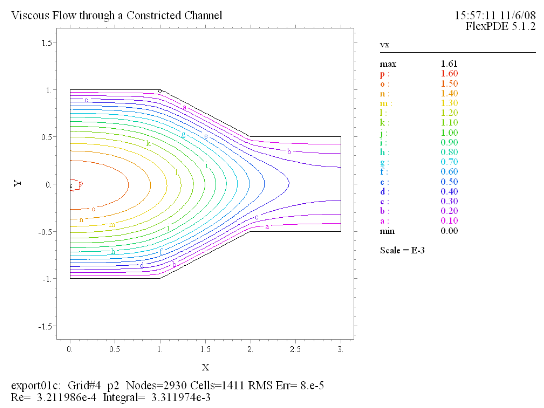
(3) Contour(vx) Report(Re) |
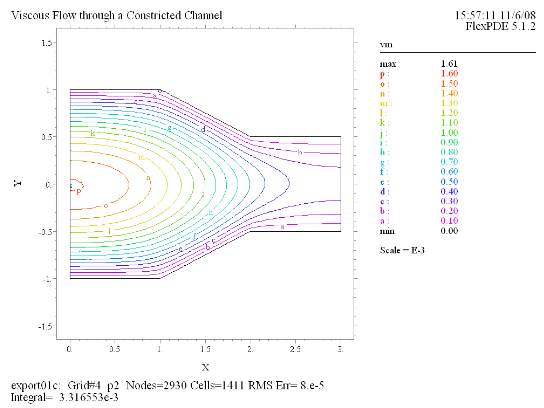
(4) Contour(vm) |
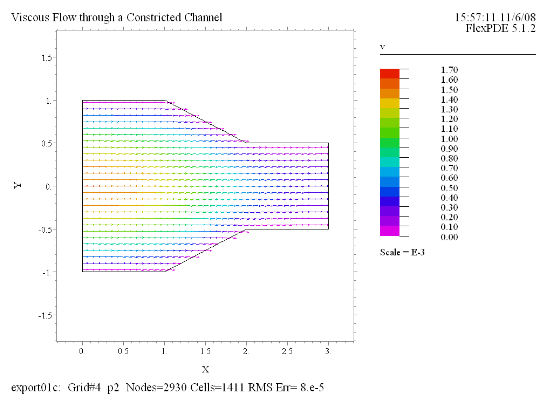
(5) Vector(v) norm |
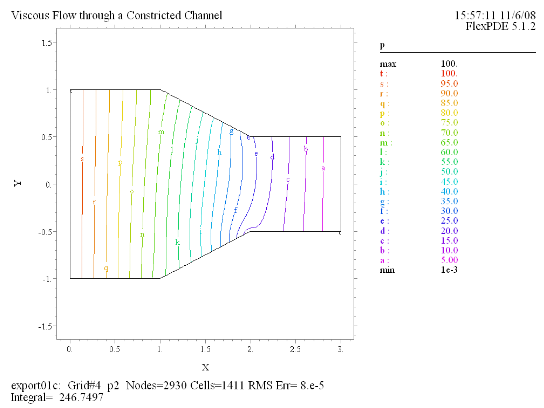
(6) Contour(p) |
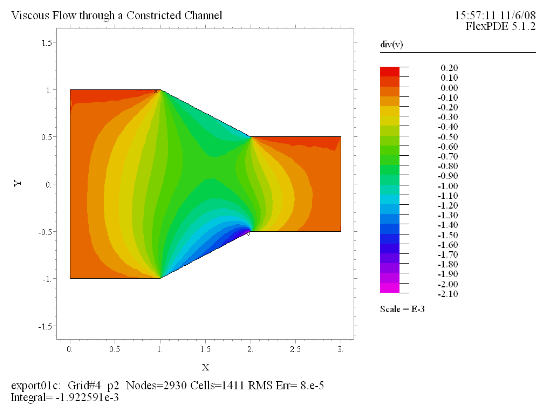
(7) Contour(div(v)) painted |
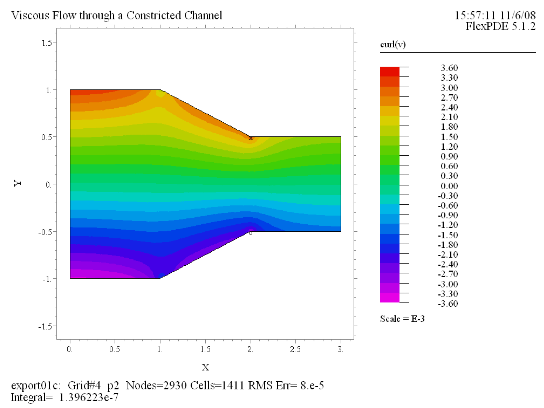
(8) Contour(curl(v)) painted |
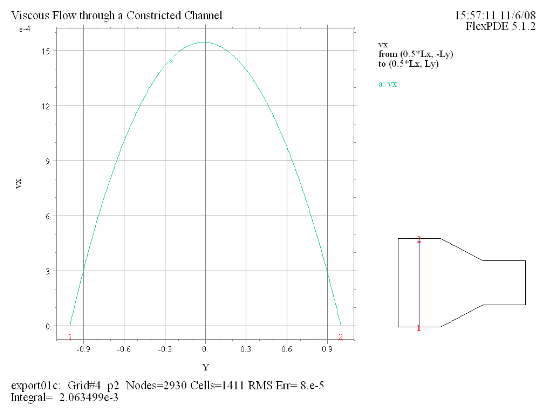
(9) Elevation(vx) from (0.5*Lx, -Ly) to (0.5*Lx, Ly) |
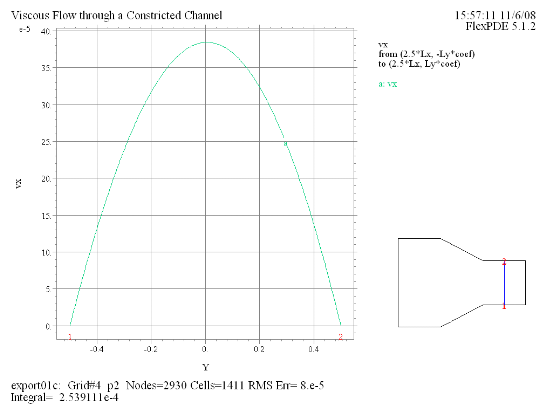
(10) Elevation(vx) from (2.5*Lx, -Ly*coef) to (2.5*Lx, Ly*coef) |

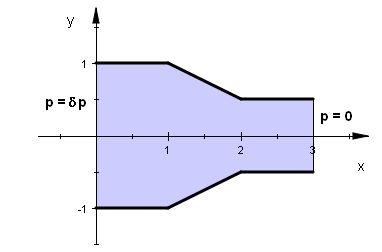 これは
これは