Stataは、マルコフ連鎖モンテカルロ法（MCMC）を利用したベイズ回帰モデルの推定をサポートしています。モデル作成においては予め用意された豊富な分布関数を利用することもできますし、独自の関数を定義して利用することも可能です。
マルコフチェーンの計算が収束した場合に限りMCMC(マルコフチェーンモンテカルロ)法によるベイズ推定の結果は適切であると考えることができます。収束状態を判断する方法の一つとしてシミュレーションで複数のチェーンを比較するという方法があります。
Stata 16以降のバージョンではbayes:プリフィックスとbayesmhコマンドのnchains()オプションを使用できます。
具体的な使用例例えば次のように入力します。. bayes, nchains(4): regress y x1 x2
このコマンドにより4つのチェーンが作成されます。
この4つのチェーンを組み合わせてより高精度な推定結果を求める事も可能ですが、それらのチェーンを視覚的に比較して収束状況を確認します。
収束の確認にはGelman–Rubinの診断法が利用できます。
複数チェーンのシミュレーションを実行したあとでbayes: regress など、いくつかの推定コマンドを実行すると、この診断結果も報告されます。
収束しない事に関心がある場合はbayesstats grubin コマンドを利用します。
これはモデルに含まれる各パラメータに対して個別にGelman–Rubinの診断を実行します。
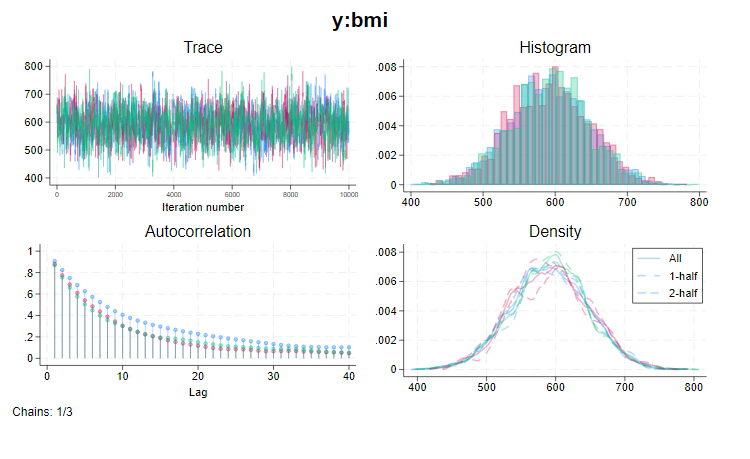
ベイズ予測とは事後予測分布を利用してシミュレーションを行うものです。この手法はモデルのフィットを吟味し、アウトオブサンプルの予測に適しています。
bayesmhコマンドでモデルをフィットした場合、bayespredict コマンドを利用することでシミュレーションの予測値やその関数を計算し、それらを新たなデータセットとして保存できます。
例えば次のように入力します。
具体的な使用例例えば次のように入力します。
. bayespredict (ymin:@min({_ysim})) (ymax:@max({_ysim})), saving(yminmax)
このコマンドはシミュレーションした値の最大/最小値を求めます。この他にも予測値の要約統計量を調べる場合にbayesgraphなどの推定後に利用するコマンド群が用意されています。
bayespredictコマンドは数千個のシミュレーション値から新たなデータセットを作成します。
もちろん、全てのシミュレーション値が必ずしも必要とは限りません。
そのようなケースでは事後分布による要約統計量として平均や中央値などをbayespredict, pmean, bayespredict, pmedianといったコマンドで求めることができます。
また、シミュレーション値からのランンダムサンプリングもサポートしています。
モデルの適合度を評価する場合には、事後分布による予測p値(PPP/ベイズ予測p値)を利用します。
PPPは観測値とシミュレーション値の一致度を計測する指標であり、新しいコマンドbayesstats ppvaluesを用いて求めます。
さらに詳しくは無料ウェビナー／分析機能例題集で！
bayes:プリフィックスbayes:を入力Stata is a registered trademark of StataCorp LLC, College Station, TX, USA, and the Stata logo is used with the permission of StataCorp.
ISO27001(ISMS)認証
情報セキュリティ・マネジメントシステム
© 2025 Lightstone Corp. All Rights Reserved
