Stata分析機能例題集
項目応答理論（IRT）

この例では、バイナリデータを使ってIRT分析を行い、irtコマンドの事後評価機能を紹介します。

データの確認

De Boeck and Wilson（2004）による、数学の能力に関するデータを使用します。
生徒はテストを受け、正解した場合1、不正解だった場合0と記録されます。
下記のコマンドで例題用のサンプルデータ「masc1」を入手し、1行目から5行目までの内容を確認します。

以下の表が表示されます。

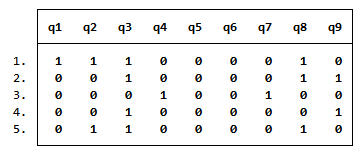
この表は、生徒1が問いq1、q2、q3、q8に正解し、生徒2がq3、q8、q9に正解したことを表しています。
生徒3以降も同様に、「1」が正解したことを表しています。
この検定の目的は、生徒の数学の能力を評価し、たとえば優・良・可のようなグループに生徒を分けることです。
各生徒の総合点は分かっていますが、総合点は試験の構造に依存するという問題点があります。
もし試験が簡単な問題で構成されていたら、ほとんどの生徒は優の評価になるでしょう。
逆に、難しい問題ばかりであれば、多くの生徒が可の評価になります。
モデルがデータにフィットする際に、IRTには、測定誤差を除いてパラメーター推定が不変であるという利点があります。
能力の推定値は試験に依存せず、項目パラメーターはグループに依存しなくなります。

バイナリデータに1PLモデルと2PLモデルをフィットさせる

下記のコマンドで、1パラメータロジスティックモデル（1PLモデル）をバイナリデータq1からq9にフィットさせます。

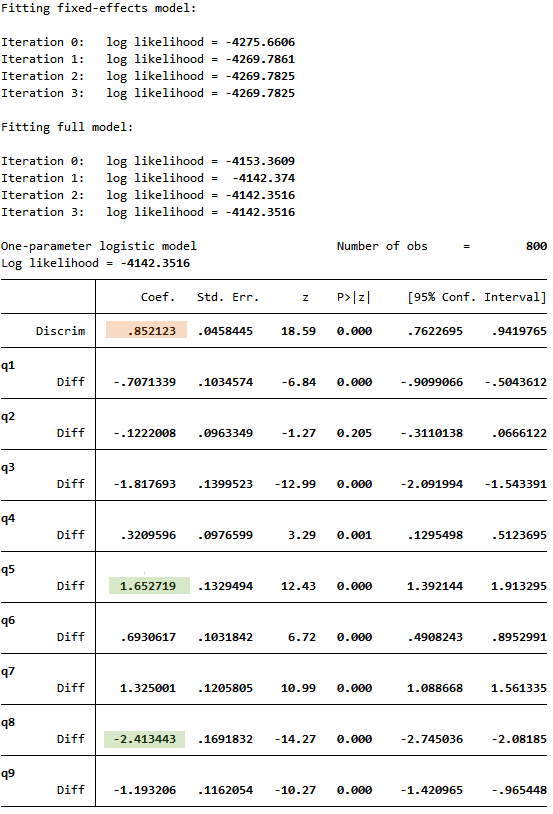
出力された表をみると、最初の行に困難度の識別パラメーター（Descrim）があります。
1PLモデルでは、このパラメーターは全ての項目で共有されます。
0.85という推定値は、この項目が完全な識別能力があるわけではないことを示しています。
つまり、特定の困難度の推定値付近では、異なる能力を持つ2人が項目に対して似たような応答をする可能性があります。
残りの行では、各項目に対して困難度のパラメーターの推定値（Diff）が表示されています。
項目の困難度のスペクトラムが広範囲に渡っていることがわかります。
最低値はq8 のb^ 8=-2.41で、最高値はq5 のb^ 5=1.65となっています。

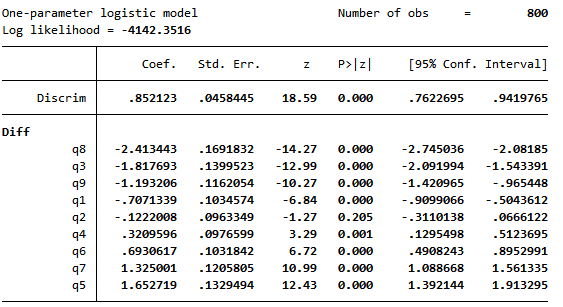
結果を指定した順番で並び替えるためにestat reportコマンドを使います。
この例では、困難度が低い項目から高い項目の順番に並べます。

項目応答曲線（ICC）とテスト特性曲線（TCC）を作成する

困難度のスペクトラムを表すために、項目応答曲線（ICC）を描きます。

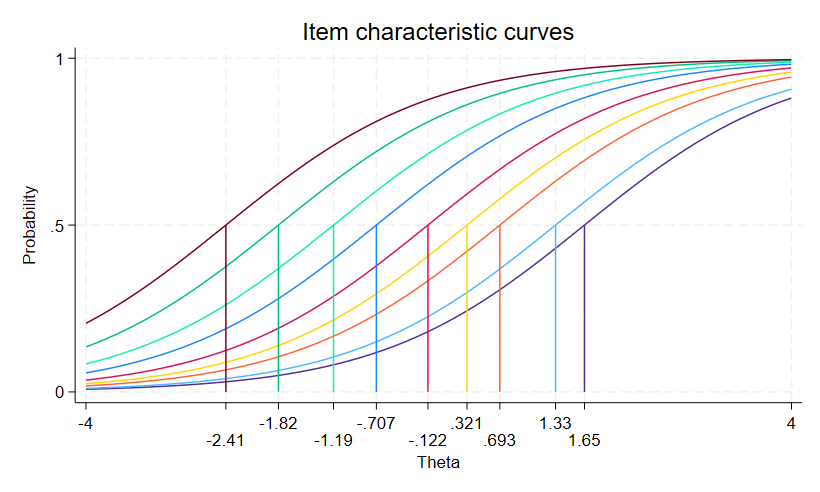
潜在能力θに対する、各項目の正答確率を表しています。1PLモデルでは、各項目の50%確率は、困難度パラメーターの推定値に対応します。
確率の合計を計算すると、テスト全体で期待される点数がわかります。
この潜在特性に対する期待される点数をプロットした図は、テスト特性曲線（TCC）と呼ばれます。
TCCを作成するには、irtgraph tccコマンドを使います。
scorelines(2 7)オプションは、期待される点数2と7に対応するプロットに線を引きます。

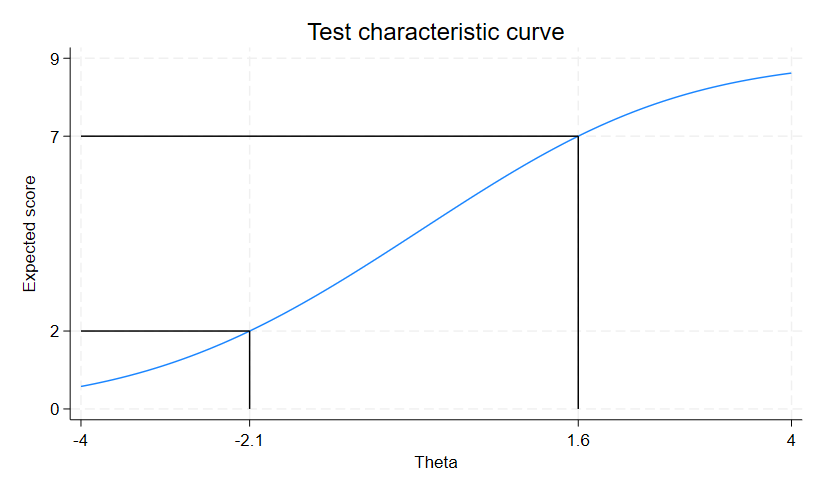
推定されるTCCによると、期待される点数が２の場合の潜在特性は-2.1、7の場合は1.6です。
IRTの不変性プロパティは、モデルがデータに適合する場合のみ保持されます。
フィットを確認する非公式な方法のひとつは、ICCに経験的比率empirical proportionsを重ね合わせることです。
予測されたICCが経験的比率に沿っている場合、モデルがフィットしていると考えられます。
経験的比率を計算するには、潜在特性を予測し、潜在特性によって項目をcollapseします。
そして、intgraph iccコマンドにaddplot( )オプションを使用して、ICCに重ねます。

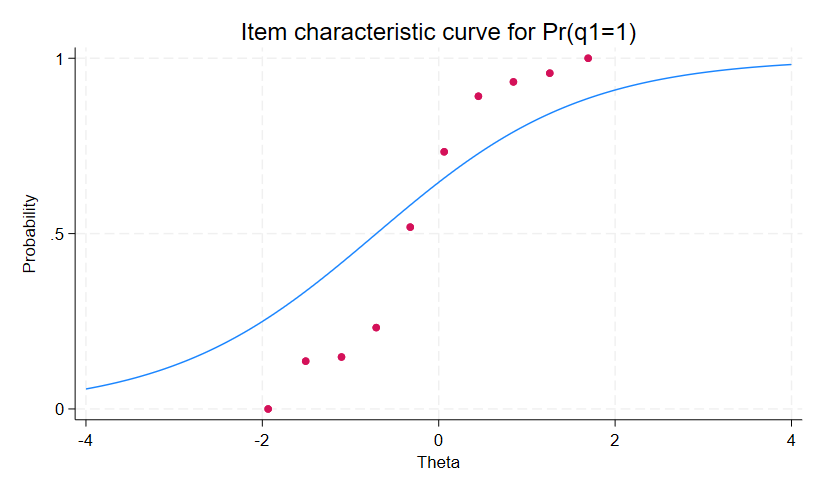
モデルの中の全項目について、経験的確率がICCにフィットしていないことが分かります。
この項目については、2PLモデルを適用した方が良いかもしれません。
2PLモデルを適用する前に、ここまでの推定をonepとして保存しておきます。

2PLモデルを適用するには、下記のコマンドを入力します。

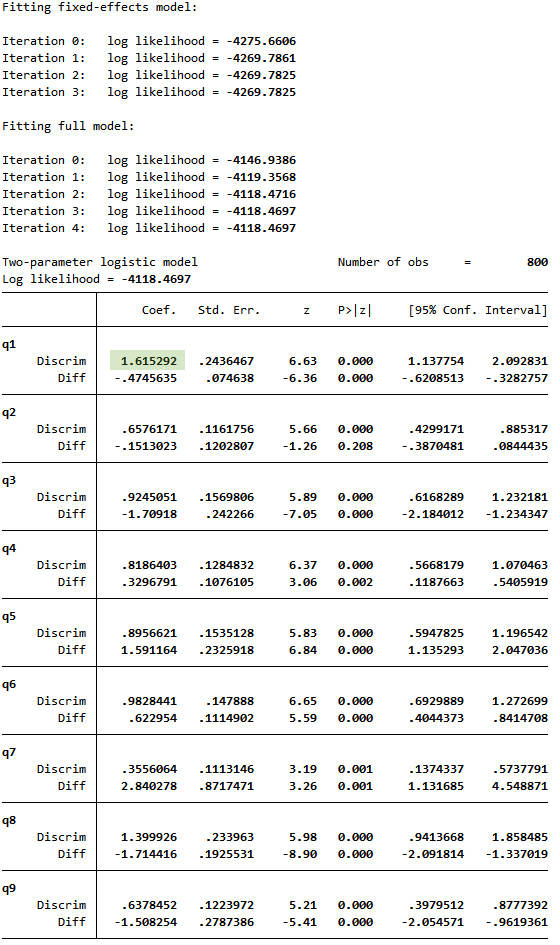
2PLモデルでは、各項目ごとに識別パラメーターがあります。
1PLモデルでは、全ての項目で共通の識別パラメーターの値が0.85と推定されました。
出力結果の表によるとq1の識別パラメーターは1.62と推定されており、経験的確率のグラフの傾きが大きいことによりフィットしているといえます。
1PLモデルは2PLモデルにネストされているので、尤度比検定を実行することでどのモデルがより適しているかを調べることができます。

有意水準がほぼゼロなので、識別パラメーターが各項目ごとに分かれていることを示しています。
2PLモデルで、潜在特性を推定するための項目の情報量をプロットすることができます。
潜在特性に対する項目情報のグラフは、項目情報関数（IIF）と呼ばれます。
モデルで全項目のIIFを出力するには、irtgraph iifコマンドを使います。

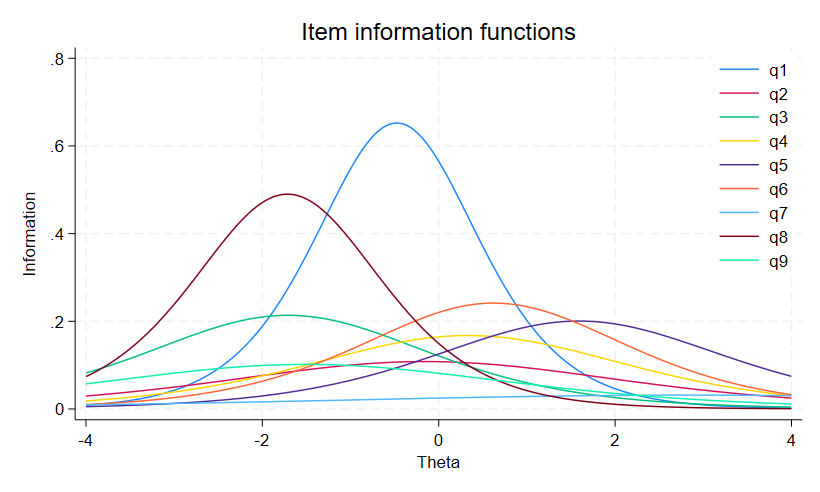
2PLモデルの場合、IIFには単峰性と対称性があります。
IIFの高さ（困難度パラメーターの項目の情報の量）は、各項目の推定された識別力に比例します。
項目q1とq8は、最も大きな識別力があり、急な傾きを持っています。
尺度の信頼性を調べるテスト情報関数（TIF）を得るために、IIFの和を求めます。

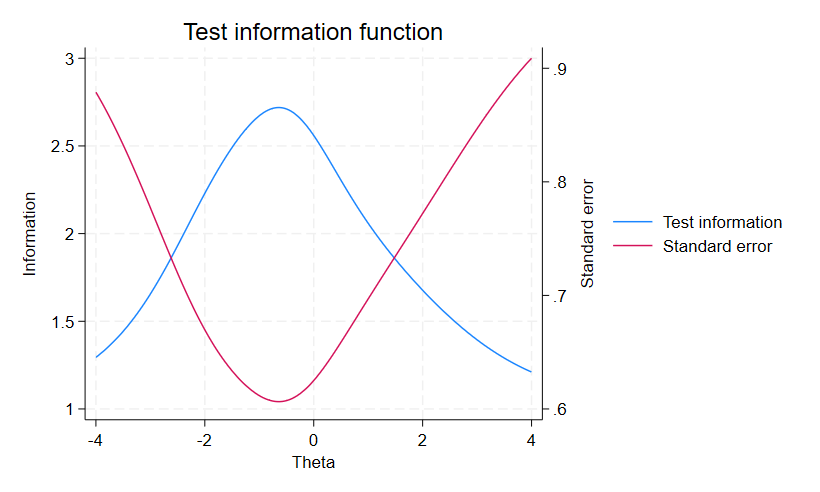
このテストは、θ=-0.5 の位置にいる人に最大の情報量を提供することが分かります。
θが-0.5 から外れると、TIFの標準誤差が大きくなり、提供される情報量が少なくなります。
バイナリモデルには、1PLモデルと2PLモデル以外にも3PLモデルがあります。
3PL モデルは、推測の可能性に対応することによって、2PLモデルに追加されます。

カテゴリカルなIRTモデルには、順序付きの応答モデルと順序なしの応答モデルが含まれます。
ここでは、順序付きの段階反応モデル（GRM）を扱います。
GRMはカテゴリカルな結果に対応するための、2PLモデルの拡張モデルです。

データの確認

モデルを描くために、Zheng and Rabe-Hesketh（2007）のデータを使用します。
このデータにはta1からta5までの5項目のアンケートの質問があり、慈善団体に対する信念と信頼を測っています。
反応は、強く同意する(0)、同意する(1)、同意しない(2)、全く同意しない(3)の4段階です。
高い点数であるほど、不信感が強いことを表しています。
5つの質問のデータを見てみましょう。

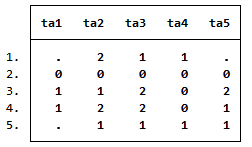
最初の行を見ると、この回答者はta1とta5には無回答、ta2には2、ta3とta4には1と回答しています。
irtコマンドは、観測値のない項目を尤度計算から除外しますが、他の欠測していない項目は残します。
モデルから欠測値のある人のデータ全てを除外するには、listwiseオプションを使用します。

カテゴリカルデータに段階反応モデル（GRM）をフィットさせる

下記のコマンドでGRMをフィットさせます。

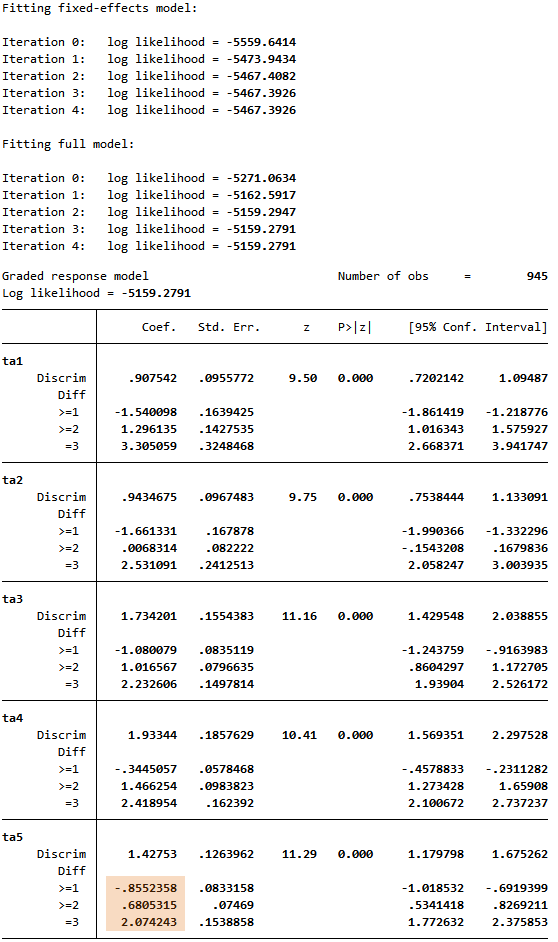
GRMは累積確率で算出されるため、推定されたカテゴリの困難度は、特定の困難度と等しい能力を持つ人物が、指定されたカテゴリ以上の困難度に応答する確率が 50％であることを示しています。
例えば、ta5において、θ=-0.86の人が0と回答する確率は50％であり、1以上と回答する確率も同じく50％です。
θ=0.68の人は0または1と回答する確率は50％で、2または3と回答する確率も50％です。θ=2.07の人は、2以下と回答する確率は50％で、3 と回答する確率も50％です。
irtgraph iccコマンドを使って、これらの確率をグラフにします。
ここでは、ta5について推定されるカテゴリの困難度と確率をプロットします。
GRMでは、各カテゴリの中間確率は推定されたカテゴリの困難度に相当します。

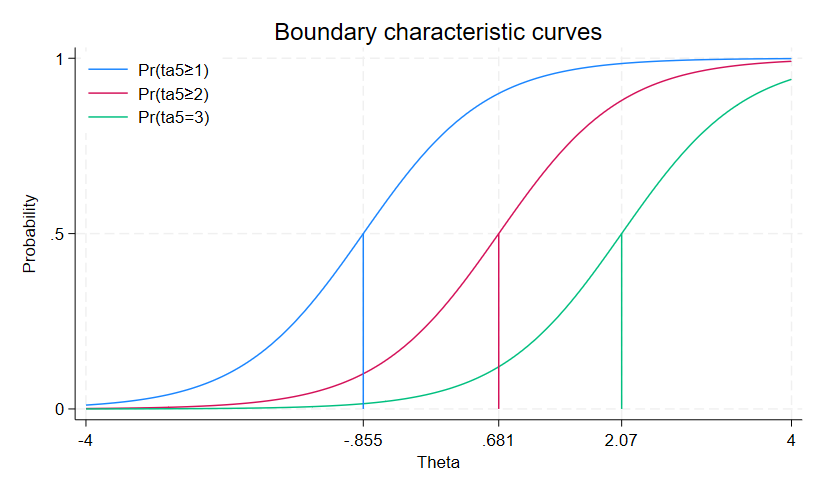
カテゴリカルな項目で特性曲線を描いた場合は、境界特性曲線（BCC）と呼びます。

項目情報関数（IIF）、境界特性曲線（BCC）、項目情報関数グラフ（CCC）を作成する

カテゴリkを選択する回答者の確率をプロットすることもできます。
カテゴリカルな項目の場合、これは項目情報関数グラフ（CCC）と呼ばれます。

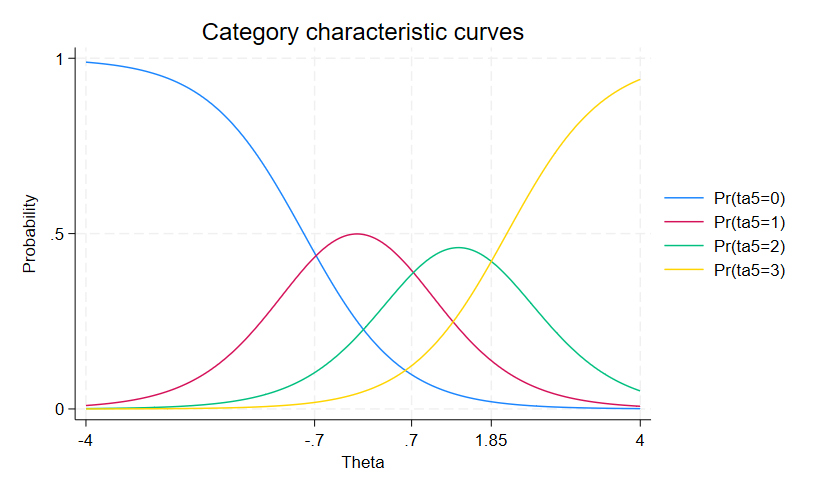
カテゴリが交差する点は、あるカテゴリから隣のカテゴリに遷移することを示しています。
つまり、不信感のレベルが低い回答者（約θ=-0.7以下の回答者）はta5について最初のカテゴリ（0：強く同意する）をほとんど選択する傾向にあります。
中間のθ=-0.7からθ=0.7の人は、ta5について2番目のカテゴリ（1：同意する）を選択する傾向にあります。
最初の例のように、全体のテスト特性関数をプロットできます。

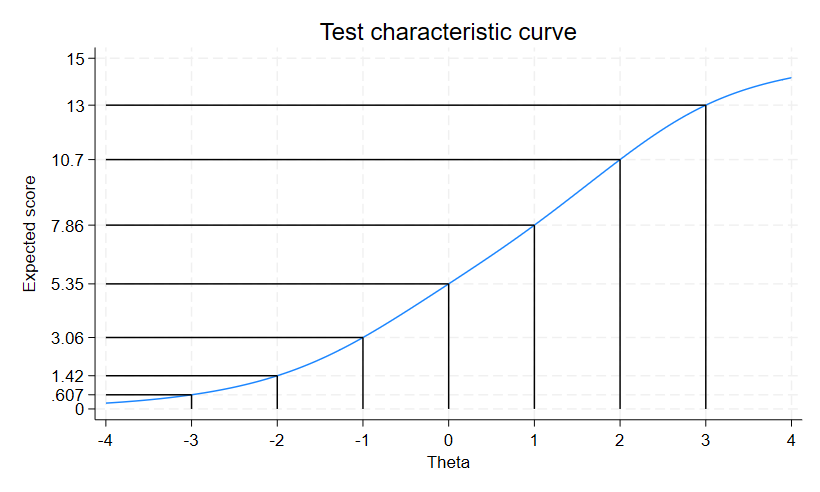
項目は5つあり、各スコアは最小値0から最大値3までなので、全体のスコアは0から15までの範囲になります。
θの値の違いによるスコアの違いを、irtgraph iifコマンドでプロットします。
θ=-3以下の場合、期待されるスコアは1以下です。
これは、θ=-3以下に該当する回答者が、全ての項目で0を選択する可能性が最も高いことを示しています。
カテゴリカルな項目の場合、項目情報関数は単峰性や対称性を示しません。
何故なら、各カテゴリは独自の情報を持っていて、それぞれが異なる範囲で最高値を取る可能性があるからです。
下記のグラフで確認しましょう。

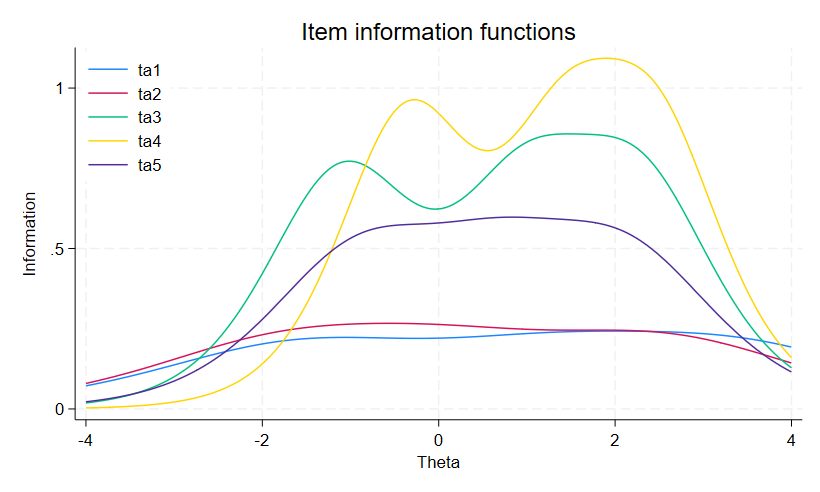
テスト情報関数は各IIFの和なので、このプロットにも山と谷があります。

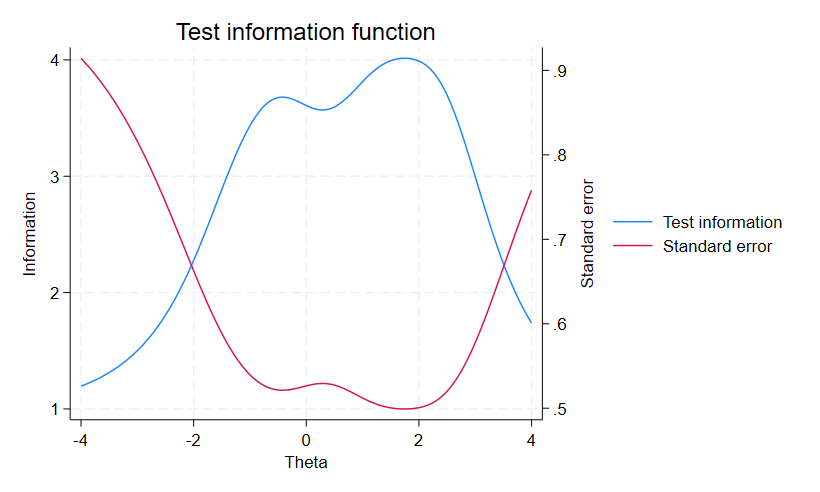
上記の例では、GRMを実行しました。
irtコマンドは、カテゴリカルな反応に対して次のようなモデルをサポートしています。

• irt nrm ： 標準応答モデル（NRM）
• irt pcm ： partial credit モデル（PCM）
• irt rsm ： rating scale モデル（RSM）

バイナリIRTまたはカテゴリカルIRTモデルに加えて、irtコマンドでさらに別のモデルを適用することもできます。
項目をサブセットし、全体に対して単一のキャリブレーションを行うためのモデルirt hybridがあります。