Stataを使いはじめる: (6)線形回帰をおこなう
6 線形回帰をおこなう
■ 線形回帰を実施し、結果を表示する
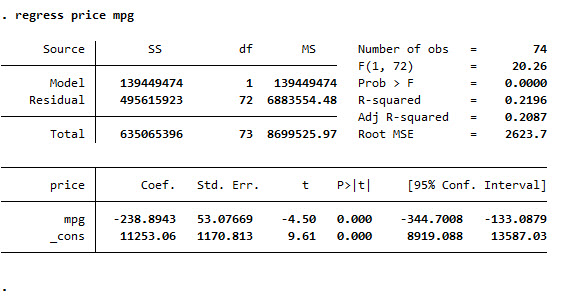
6.結果を順に詳しく見ると、まず左上にはANOVAテーブルがあります。これらの値は、F分散比や決定係数の計算に用いられます。
| Model SS | 回帰平方和または回帰変動と呼ばれます。 全変動のうち回帰モデルによって説明された変動を示します。 |
| Residual SS | 残差平方和または残差変動とよばれます。 全変動のうち回帰モデルによって説明できなかった変動を示します。 |
| Total SS | 全平方和または全変動と呼ばれます。従属変数の値のばらつきを示します。 全変動 = 回帰変動 + 残差変動 となります。 |
| Model df | モデルの自由度です。説明変数に掛けられる係数の個数です。 |
| Residual df | 残差の自由度です。全体の自由度からモデルの自由度を引いて求めます。 |
| Total df | 全体の自由度です。データの行数によって定まります。 定数項ありの場合、データ行数 - 1 となります。 定数項なしの場合、データ行数 となります。 |
| Model MS | モデルの平均平方です。回帰変動をモデルの自由度で割って求めます。 1自由度あたりの回帰変動を意味します。 |
| Residual MS | 残差の平均平方です。残差変動を残差の自由度で割って求めます。 1自由度あたりの残差変動を意味します。 |
7.右上には決定係数、自由度調整済み決定係数などの計算結果が表示されています。
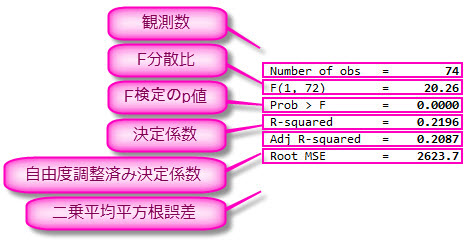
| Number of obs | 分析に使用したデータの行数(観測数)です。 |
| F(1, 72) | F検定のための検定統計量です。モデルの平均平方を残差の平均平方で割って求めます。 |
| Prob > F | F検定におけるP値です。帰無仮説「全ての係数が0である。」か検定します。 |
| R-squared | 決定係数です。全変動における回帰変動の割合を示します。 0以上1以下の値をとります。 |
| adj R-squared | 自由度調整済み決定係数です。 決定係数を自由度で調整することで、説明変数の個数が異なるモデルを比較できます。 |
| Root MSE | 残差の平均平方の平方根です。値が小さいほどあてはまりが良いと解釈します。 |
8.最下段には、係数の推定結果が表示されています。
| Coef. | 推定された係数です。回帰式が定まります。 |
| Std. Err. | 推定された係数の標準誤差です。 |
| t | t検定のための検定統計量です。係数を標準誤差で割って求めます。 |
| P>|t| | 両側検定に対するP値です。帰無仮説「係数が0である。」か検定します。 |
| Conf. Interval | 信頼区間です。信頼度は95%以外でも算出できます。 |

 前のトピック
前のトピック
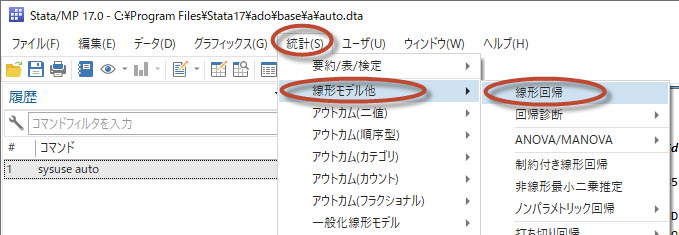
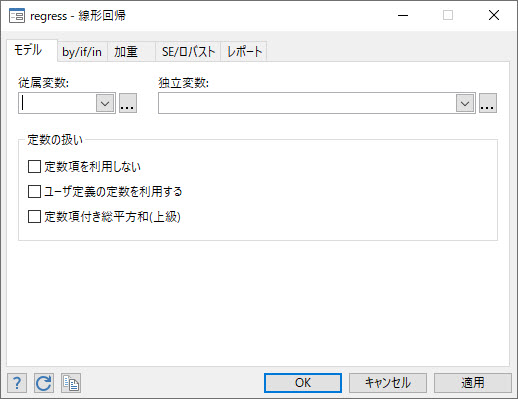
 をクリックし、プルダウンから従属変数とする変数(次の例では price)をクリックします。
をクリックし、プルダウンから従属変数とする変数(次の例では price)をクリックします。