ベイズブートストラップ
ルービン(1981)によって提案されたベイズブートストラップ法は、ベイズの定理を活用した手法であり、 従来のブートストラップ法に代わる手法です。 ベイズブートストラップ法では、観測値を含めるか除外するかを決定する復元抽出ではなく、 ディリクレ分布から各観測値の寄与度に対して確率重みを割り当てます。 このアプローチは、各観測値の寄与度を連続的な確率重みで表現し、母集団の不確実性をなめらかにモデル化します。
ベイズブートストラップ法は、各観測値の寄与度に対する事後分布を与えるものとして解釈できます。 このベイズ的枠組みにおいて、研究者は各観測値に重みを割り当てる際に、事前知識を反映することができます。 さらに、従来のブートストラップ法は各観測値を含めるか否かの離散的な寄与度しか利用しないのに対し、ベイズブートストラップ法では観測値の寄与度を連続的に取り扱います。 これにより、ベイズブートストラップ法は、共線性をもつ観測値が繰り返し選ばれる状況や、カテゴリ全体が代表されない状況など、 従来のブートストラップ法における特定の問題の影響を軽減できます。
bayesboot コマンドは、ディリクレ分布から各観測値の寄与度の重みを生成し、
パラメータと統計量の推定に用いることで、ベイズブートストラップ法を行います。
デフォルトでは、各観測値は平等に扱われますが、priorpowers() オプションを用いることで、
観測値に対してより有益な事前確率を含めるようにカスタマイズできます。
bayesboot は、既存の bootstrap プレフィックスと同様に、
公式コマンドおよびコミュニティ提供コマンドとシームレスに連携します。
復元抽出によって生じる不安定性の回避
ベイズブートストラップ法は、モデルの仮定を置かずに推定の不確実性を評価する、いわばブートストラップのベイズ版です。
結果の信頼性を確認するためには、どのような状況でも通常のブートストラップ法と併せて結果を比較・検証するのが望ましいといえます。
通常のブートストラップでは、復元抽出によって同じサンプルが繰り返し含まれることからくる不安定性に注意が必要です。
一方で、ベイズブートストラップ法はそうした不安定性を回避できます。
ただし、両者は不確実性の捉え方が異なるため、単純な優劣の問題ではありません。
そのため、それぞれの手法で得られる推定結果を比較し、どの程度一致しているか、どこが異なるかを丁寧に吟味することが重要です。
Stata19 の bootstrap コマンドおよび bayesboot コマンドでは、
各手法をコマンド一行で実行することができます。
操作例
ベイズブートストラップと従来のブートストラップ法
線形回帰の回帰係数にベイズブートストラップ法と従来のブートストラップ法を適用し、比較してみましょう。 auto データセットを用いて、車両価格(price)と修理記録(rep78)が燃費(mpg)にどのように影響するかを分析します。
まず、既存のbootstrapプレフィックスを用いて従来のブートストラップ法を実行し、
次に新しいbayesbootプレフィックスを用いてベイズブートストラップ法を実行します。
再現性を確保するため、どちらの場合も rseed(111) オプションを指定します。
. sysuse auto. drop if rep78 == .. bootstrap, rseed(111): regress mpg price i.rep78
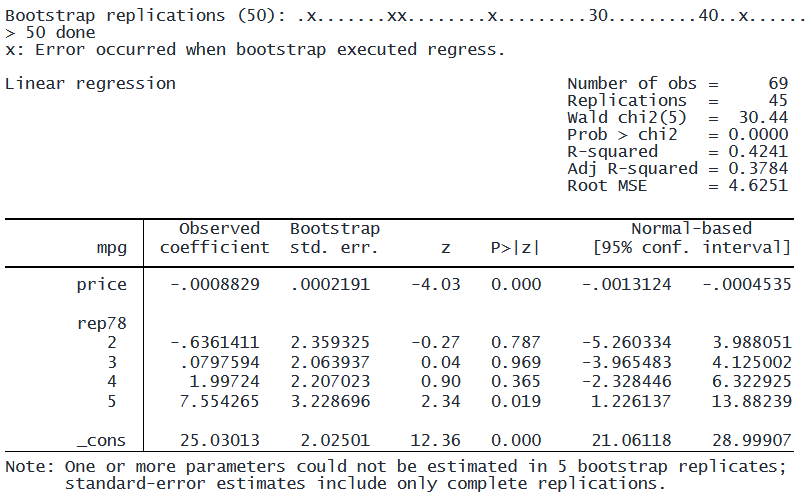
次に、ベイズブートストラップ法を用いて同じ分析を実行します。
また、bayesbootの generate() オプションを指定して、生成された重みを新しい変数iw1からiw50に保存し、
後で比較できるようにします。
. bayesboot, rseed(111) generate(iw): regress mpg price i.rep78
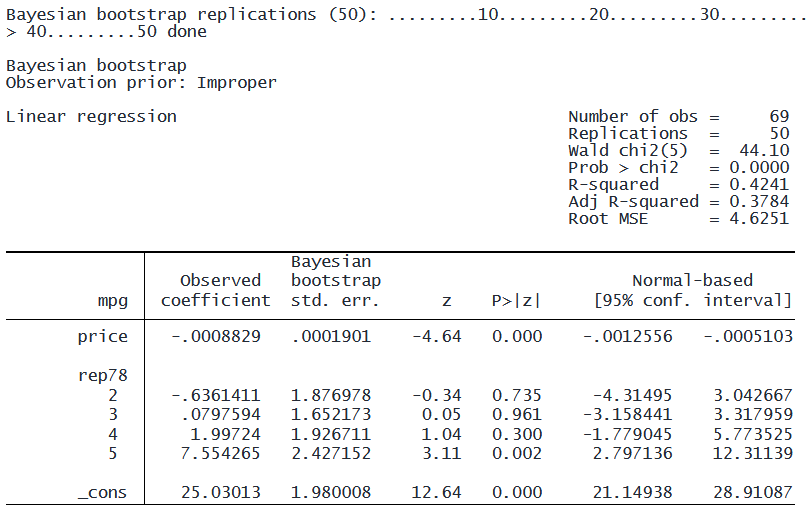
どちらの手法も全体的には同様の結論になりますが、再現性の出力からベイズブートストラップ法の利点が見て取れます。
従来のブートストラップ法の結果に「x」マーカーが付いていることに注目してください。
これらのマーカーは、反復計算ができなかったことを示し、結果として、それらの反復における回帰係数推定値が欠損値となります。
これは、完全共線性のため、または rep78 のカテゴリの一部に観測値がないために発生しています。
一方、bayesboot は50回の反復すべてをエラーなく完了します。
この安定性の向上は、従来のブートストラップ法の離散的な復元抽出ではなく、 ベイズブートストラップ法が連続的な重みを使用しているためです。 連続的な重み付け手法は、復元抽出で時々発生する完全共線性に伴う問題を回避することで、 より高い数値的安定性を維持します。
事前情報の組み込み
ベイズブートストラップ法の主な利点の1つは、観測値の相対的な重要性や信頼性に関する情報がある場合に、 観測値の事前分布を指定することにより、ドメイン知識を組み込むことができることです。
以下では、priorpowers() オプションを使用してデフォルトの事前分布を変更することで、
異なる事前分布値が推定精度と統計的有意性にどのように影響するかを検討します。
. generate priorvar = rbeta(2,7)+2. bayesboot, priorpowers(priorvar) rseed(111): regress mpg price i.rep78
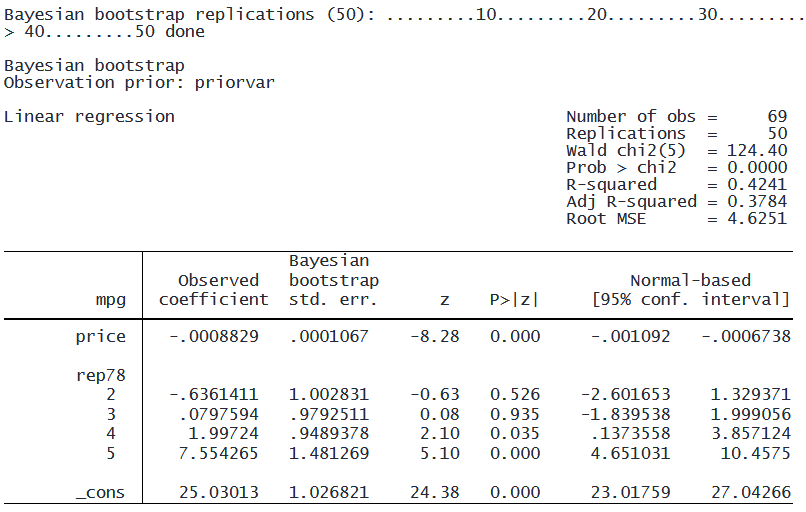
4.rep78 の係数を見ると、デフォルトの事前分布では信頼区間に 0 が含まれていますが、 カスタム事前分布では 0 は含まれていません。 これは、事前分布の値が大きいほどデータセットの代表性に対する確信が強くなり、信頼区間が狭くなるためです。
bayesboot をラッパーとして使う
bayesboot コマンドは、以下の 2 つの機能を組み合わせた便利なラッパーです。
rwgen bayes コマンド:ベイズブートストラップ法に基づいて重みを生成します。
bootstrap の iweights() オプション:推定時にこれらの重みを適用します。
前の例の bayesboot の結果を再現するには、以下の 2 つのコマンドを指定します。
. rwgen bayes myiw, priorpowers(priorvar) rseed(111). bootstrap, iweights(myiw1-myiw50): mpg価格の回帰 i.rep78
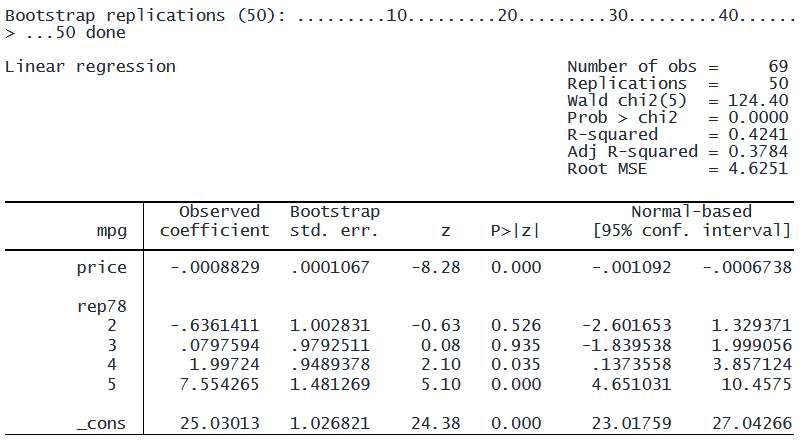
カスタム事前分布の影響
カスタム事前分布が分析にどのような影響を与えるかを理解するために、 最初の反復におけるデフォルトの重みとカスタム重みの分布を比較してみましょう。
. summary iw1 myiw1

要約統計量から、重みの分布に重要な違いが明らかになりました。 両方のセットの平均値は同じ(1/69 = 0.0144928)ですが、より高い事前分布に基づくカスタム重みでは、 変動性が大幅に低下しています。この変動性の違いは、前述のように、回帰分析の結果に直接影響を及ぼします。
参考
さらに詳しい内容につきましては、下記のマニュアルをご覧ください。


