局所平均処置効果の推定

　処置を割り当てられても、実際にその処置を受けない個人がいる場合、 つまり、処置を受けるかどうかを決める観察できない特性が存在する場合、 処置効果を識別するのは難しくなります。 (＊訳者注：ここでの「識別」とは、理論的に処置効果を一意に定められることを意味します。 識別性がなければ、推定そのものの意味付けが難しくなります。)
　しかし、時には幸運にも、割り当てられた処置がわかっていたり、 誰が処置を受ける動機を持つかを示す情報「操作変数」がわかっていたりします。 lateffectsコマンドはこの操作変数を利用して、意味のある因果効果を推定します。

　lateffects は母集団の中の特定の部分集団に対する因果効果を表す 局所平均処置効果（LATE: Local Average Treatment Effect）を推定します。
　本来、母集団全体に対する処置効果を特定したいのですが、多くの場合それは不可能です。 なぜなら、処置群と非処置群の間には観察できない差異が存在し、 母集団全体に対する処置効果は識別できないからです。観察できない要因が処置群と非処置群の間にあると、 それらが因果関係をゆがめてしまい、求めたい因果効果を正しく識別できなくなります。
　一方で、介入研究では、各個人がどの処置にランダムに割当てられたかを知ることができる場合があります。 また、観察研究では、個人が処置を受けるように「促す」二値の外生変数を利用できることがあります。 このような変数によって、母集団があたかもランダムに処置群と非処置群に分けられるような状況では、 処置割当てに従う人々（コンプライヤ : compliers）に対する効果、 すなわち局所平均処置効果（LATE: Local Average Treatment Effect）を識別することができます。 これはコンプライヤ平均処置効果 (Complier Average Treatment Effect)とも呼ばれます (訳者注：CACE: Complier Average Causal Effectとも呼ばれる)。
　共変量を含まない場合、LATEは二段階最小二乗法によって推定することができます。 しかし、共変量をモデルに組み込むと、この同値性は崩れます。 つまり、単純に二段階最小二乗法を用いるだけでは、求めたい因果効果を正しく得ることができないのです。 lateffects は、共変量の有無の両方の状況で、正しくLATEを推定するための手法を提供します。

操作例

　小学校で実施されている読解力向上を目的としたプログラムへの参加（participate 変数）が、 大学入試に使用される高校の州統一試験の得点（score 変数）にどのような影響を与えるかを調べているとしましょう。
　このプログラムへの登録は任意です。そのため、参加は無作為ではなく、 測定しようとしている効果と交絡する可能性があります。 幸いなことに、学校ごとに、プログラムに参加するグループと参加しない対照グループを選ぶ抽選が行われました。 この抽選では、低所得世帯の子どもに、より高い当選確率が与えられていました。 選ばれた学生の家庭は、参加を決めた場合、一度だけ小額の現金給付を受け取りました。
　二値変数 selected は、プログラム参加に選ばれた場合に 1 をとります。 もちろん、抽選で選ばれた全員が実際にプログラムに参加したわけではありませんし、 抽選結果の現金給付に関係なく参加した学生もいました。 もし抽選が完全に無作為であったなら、selected を操作変数として用い、 LATE（局所平均処置効果）を推定することができたでしょう。 しかし、抽選が所得に基づいて行われたことがわかっているため、 共変量で調整した後に「選抜が無作為であった」とみなせるようなモデルを指定する必要があります。
　私たちは、個人が農村地域（rural 変数）に住んでいるかどうか（この集団では都市よりも貧しい）および 低所得地域（lowinc 変数）に住んでいるかどうかを統制すれば、 操作変数が実質的に無作為に割り当てられたものとみなせると考えます。
　lateffects コマンドを使用することで、処置割り当てに従った人々に対する、 プログラム参加の試験得点へのLATEを推定するモデルを当てはめることができます。
　次のコマンドを入力しましょう：

　ここでは、正規化された κ 重み推定量（normalized kappa weighted estimator） を採用しました。 最初の括弧は結果変数に対応し、2番目の括弧は処置に対応し、 最後の括弧は操作変数に対する傾向スコアモデルに対応します。 以下のような結果を得ました：

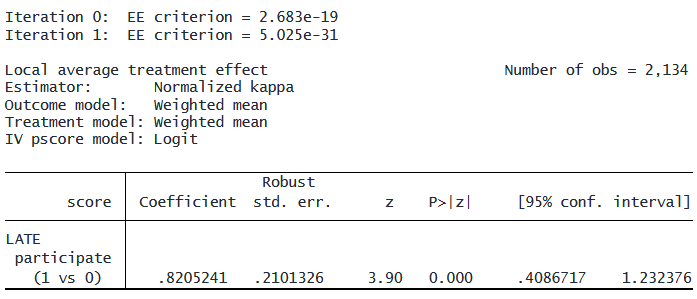
　LATE（局所平均処置効果）の値は 0.82 でした。 これは、「抽選の結果に従った学生（コンプライヤ）」という部分集団において、 「プログラムに参加した場合」の州統一試験の平均スコアは、 「参加しなかった場合」より平均して 0.82ポイント高いことを意味します。 スコアは 1 から 10 の連続的な尺度で測定されています。
　次に、2005 年時点の成績平均値（GPA） gpa2005変数 が、 処置（プログラム参加）と結果（試験スコア）の両方をモデル化する際に重要であると考えるとしましょう。 処置や結果をこのようにモデル化するためには、 逆確率重み付き回帰調整推定量（IPWRA: inverse-probability-weighted regression adjustment estimator）を 用いる必要があります。次のコマンドを入力し、次のような結果を得ました：

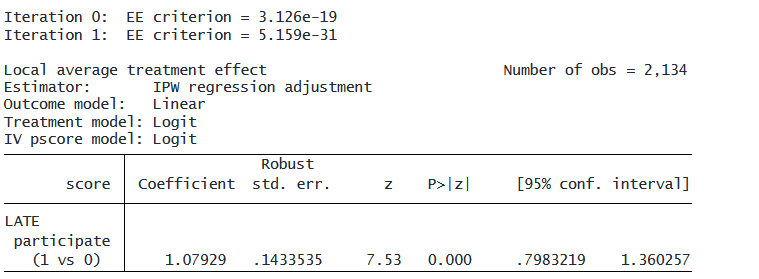
　GPAを考慮に入れると、LATEはより大きくなりました。 しかし、いずれの場合もおおよそ1 ポイント前後です。 lateffects を実行した後は、共変量で調整した後に、 処置の割当てが「調整によって擬似的に無作為化されている」かどうかを確認することができます。 そのためには、次のように入力します。

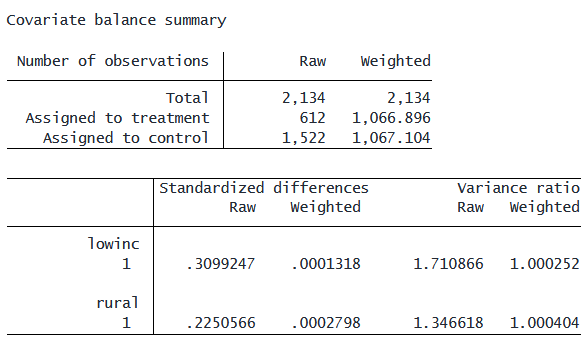
　出力の最初の表を見ると、処置群または対照群に割り当てられる確率によって重み付けを行った後では、 サンプル全体に対して両群がおおむね均衡していることがわかります。 重み付けしない場合のサンプルサイズは処置群が612件、対照群が1,522件でした。 同様に、重み付け後の標準化した差が0に近く、分散比も1に近いことが確認できます。 これは、共変量を調整した後では、処置の割り当てが「擬似的に無作為化された」状態にあることを示しています。 したがって、これは私たちのモデル設定が妥当であることを裏づけています。
　さらに、ここでできることは多くあります。上では線形モデルを当てはめましたが、 結果変数が二値、カウント、または比率である場合には、 プロビット、ロジット、ポアソン、フラクショナルプロビット、フラクショナルロジットモデルなどを 用いることができます。また、モデルの前提をさらに検証することも可能です。 たとえば、lateoverlap コマンドを使って オーバーラップの仮定が満たされているかを確認できます。 さらに、estat compliers コマンドを使えば、コンプライヤ集団における共変量の平均を調べ、 その部分集団の特徴を明らかにすることができます。

参考

　さらに詳しい内容につきましては、下記のマニュアルをご覧ください。

開発元マニュアル