多変量解析 (Proのみ)
多変量解析は、1つ以上の変数を持つデータの分析に使用され、変数同士がどのように関連し、それらを組み合わせて複数の観測例を区別するために使用されます。「多変量分析」自体は特定の分析方法ではなく、重回帰分析や主成分分析といった、さまざまな分析手法の総称です。
変量、多変量とは
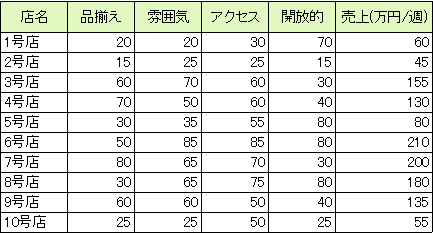
下図は、あるコンビニエンスストアチェーンの品揃え、雰囲気、アクセスの良さなどについて○か×で答えるアンケート調査を実施した結果です。アンケートで○を付けた人数とそれぞれの店舗の売上データをまとめています。このときの「品揃え」や「売上」等の項目を変量といい、複数の変量からなる資料を多変量データといいます。
多変量解析とは
上の表のような多変量データがあるとき、「6号店の売上が多い」とか「2号店は品揃えが悪い」といったことはわかりますが、それでは、個別の変量を分析した結果にすぎません。
このような場合に多変量解析を使用すると、「どの項目が、どの項目にどう影響しているか」といった、複数の変量間の関係を探ることができます。
目的は手法により異なりますが、大きく分けて「予測」と「要約」の2つがあります。
- 予測
- 要約
複数の変数から何らかの結果を予測するもので、たとえば、身長、体重から性別を予測します。
手法の例:重回帰分析、判別分析、部分最小二乗法、ロジスティック回帰など
複数の変数を少ない変数で説明するもので、たとえば、算数、理科、国語、社会という4科目のテスト結果から理系の能力と文系の能力という2つに要約したりすることです。
手法の例:主成分分析、クラスター分析、因子分析など
OriginProで実行できる多変量解析の手法
OriginProでは、以下の多変量解析の手法を利用できます。通常版のOriginでは多変量解析の機能は使用できないのでご注意ください。
- 線形多重回帰(重回帰分析)
- 主成分分析(PCA)
- クラスター分析
- 判別分析
- 部分最小二乗(PLS, Partial Least Squares Regression)
- アプリで利用可能な機能(ロジスティック回帰、因子分析、正準相関分析など)
複数の変数が結果の変数にどのような影響を与えているかを分析します。
多変量の資料から小数の特徴的な変量を合成し、データを分析します。
異なる性質のものが混ざり合った集団から、互いに似た性質をもつものを集めていくつかのグループに分けます。OriginProでは階層型と非階層型(K-means法)のクラスター分析を利用できます。
どの群に属しているかが分かっている標本があるときに、まだ分類されていない標本がどちらの群に属するかを推定する手法が判別分析です。
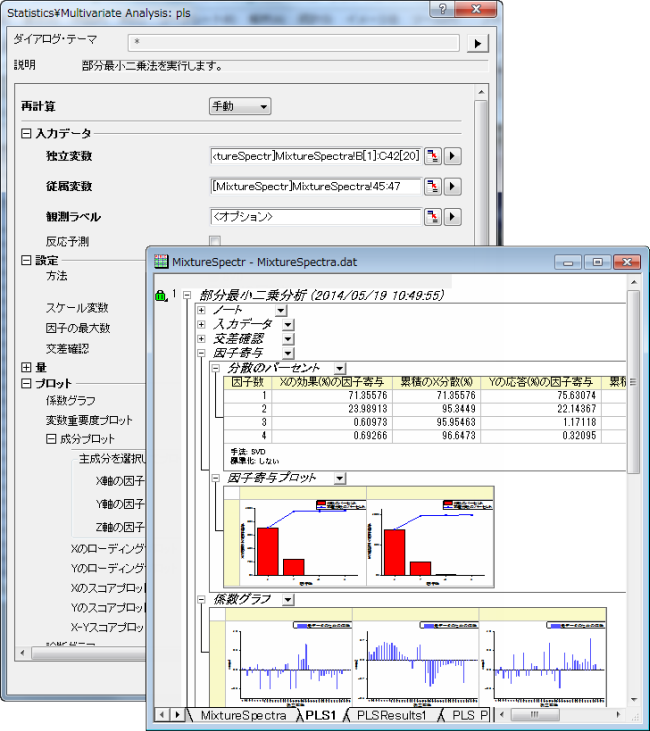
重回帰分析のように、複数の変数が結果の変数にどのような影響を与えているかを分析しますが、多重共線性のあるデータでも予測精度を向上させることができるという点に違いがあります。
必要に応じてOriginProの機能を拡張できるアプリを使用すれば、標準機能で利用できない多変量解析の様々な手法を利用できます。
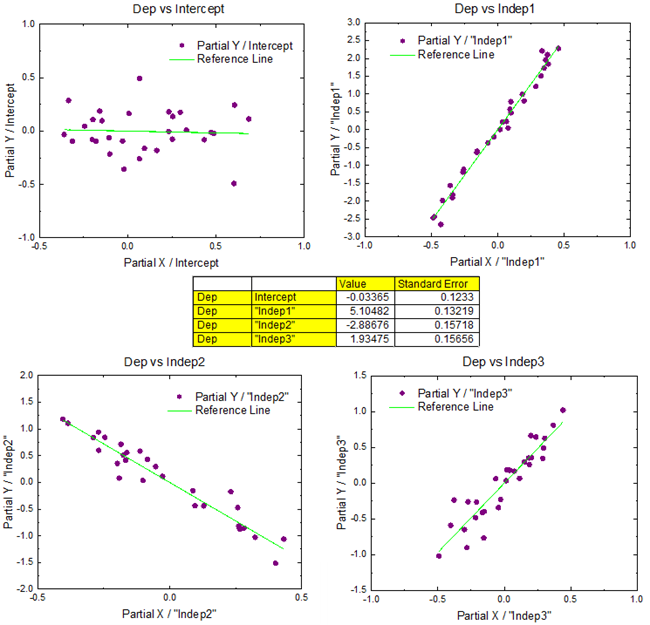
線形多重回帰(重回帰分析)
重回帰分析は、1つの目的変数を複数の説明変数で予測しようというものです。説明変数の変動によって目的変数の変動がどの程度影響されるかを分析します。
最小二乗法により、y = a + b1*x1 + b2*x2 + … + bn*xn という重回帰式を求めます。
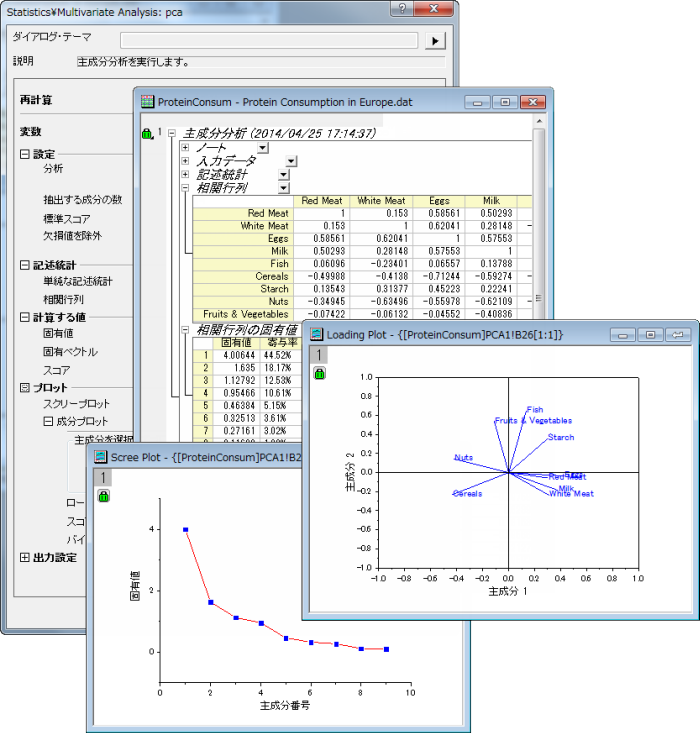
主成分分析
クラスター分析
クラスター分析は、性質の異なる大きなデータセットを似たような特性を持った小さなグループ(クラスター)に要約します。大きな変数や観測値がある場合にその関係性を見つける際の効果的な分析手法です。
Originは、以下2通りのクラスター分析を提供しています。
- K-Means法クラスター分析
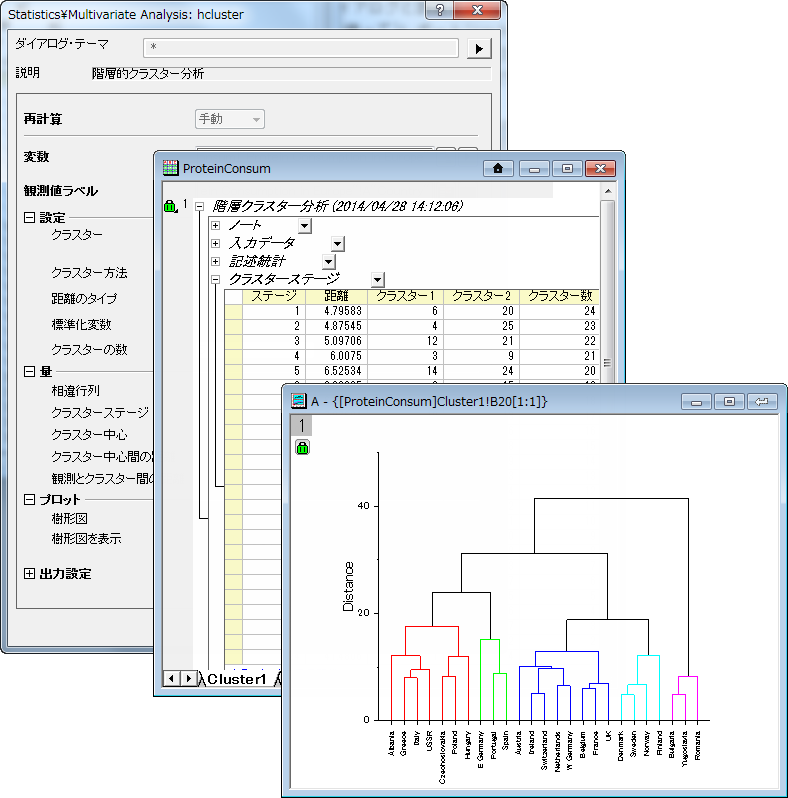
- 階層的クラスター分析
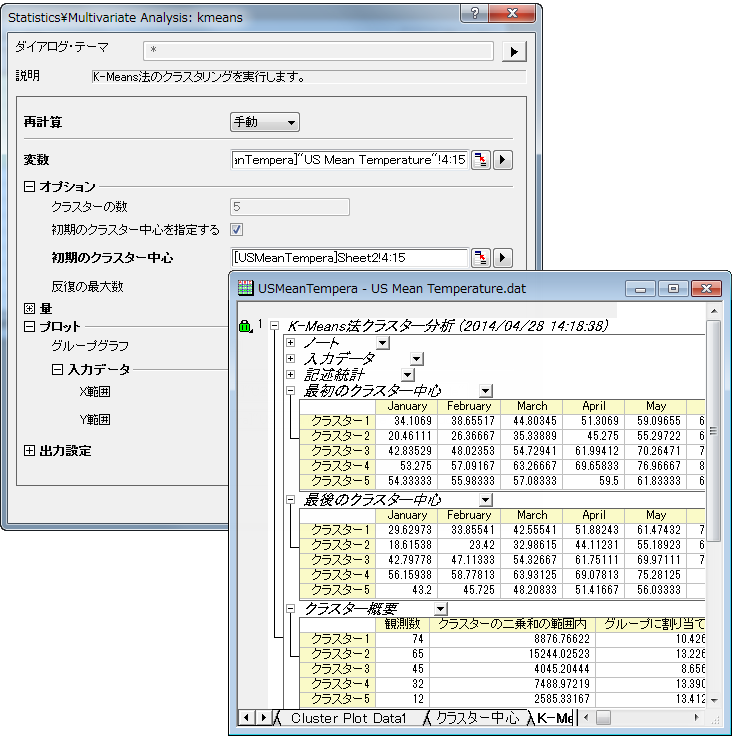
K-Means法クラスター分析では、K個のクラスターを使用して観測値を分類します。この方法では、データとクラスターの中心との距離を最小になるようにします。K-Means法分析はクラスター分析の中では簡単なアルゴリズムの使用する方法なので、階層的クラスター分析よりも早く分析が可能です。
一般に、サンプルサイズが100を超える場合にK-means法を使用します。しかし、この方法の場合、クラスターの数または観測値の中心が分かっていることを前提としています。
この方法では、各要素がその類似性や距離の程度によって段階的に分類されます。クラスターの数は、樹形図から決定することができます。
階層的クラスター分析は変数、観測値(カテゴリデータ)、連続変数を分析するのに適していますが、K-Means法に比べて解析に時間がかかります。
判別分析
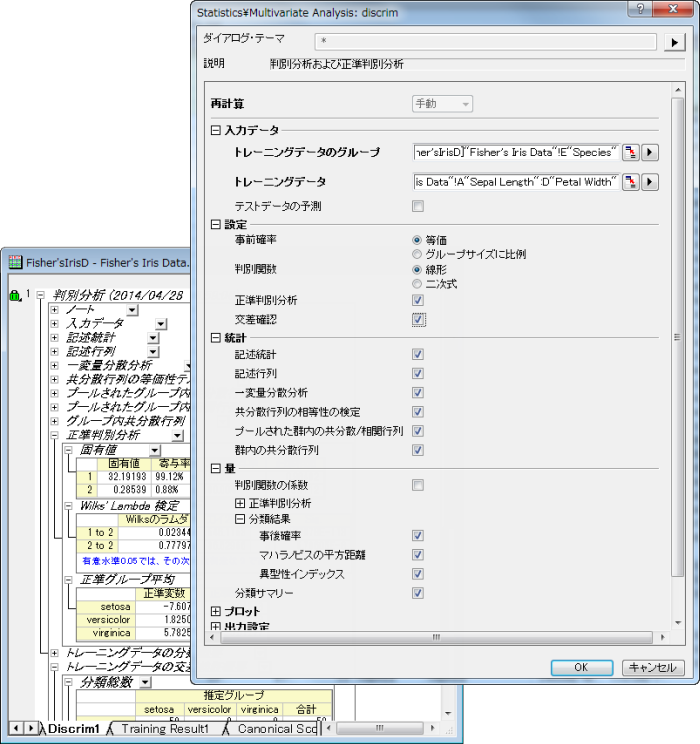
判別分析は、明確な違いがある観測値を識別し、新たな観測データを既存のグループに分類するために使用されます。この方法は生物学の種の分類や、医学分野における腫瘍の分類、顔認識のテクノロジー、クレジットカードや保険業界でリスクを割り出すのに使用されます。
判別分析を行う場合、2つの大きな目的があります。
- 識別
- 分類
既に分類のわかっている全ての観測データを使用して分類子を組み立てる
分類子を使用してグループ分けされていないデータを分類する